Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 35.6 Мордкович — Подробные Ответы
а) Запишите поочерёдно коэффициенты подчёркнутых одночленов.
б) Составьте таблицу распределения коэффициентов, найденных в пункте а).
в) Составьте таблицу распределения процентных частот.
г) Постройте круговую диаграмму распределения процентных частот.
а)
\[
6,\ 4,\ 1,\ 6,\ 6,\ -1,\ 6.
\]
б)
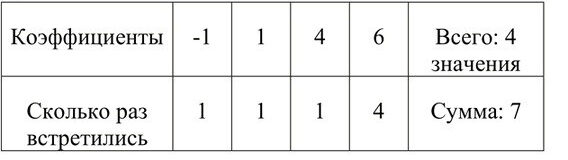
Построим таблицу абсолютных частот, то есть подсчитаем, сколько раз каждое уникальное значение встречается в выборке.
Сначала выделим все различные значения:
\[
-1,\ 1,\ 4,\ 6.
\]
Теперь посчитаем их количество:
— Значение \(-1\) встречается 1 раз,
— Значение \(1\) — 1 раз,
— Значение \(4\) — 1 раз,
— Значение \(6\) — 4 раза (в позициях 1, 4, 5 и 7).
Проверим: \(1 + 1 + 1 + 4 = 7\) — совпадает с объёмом выборки.
Таблица абсолютных частот:
в)
Теперь перейдём к относительным частотам, выраженным в процентах.
Объём выборки \(n = 7\).
Для каждого значения вычислим:
\[
\text{частота, %} = \frac{\text{количество встреч}}{7} \cdot 100\%.
\]
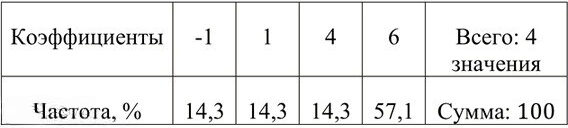
— Для \(-1\): \(\frac{1}{7} \cdot 100\% \approx 14{,}2857\% \approx 14{,}3\%\),
— Для \(1\): \(\frac{1}{7} \cdot 100\% \approx 14{,}3\%\),
— Для \(4\): \(\frac{1}{7} \cdot 100\% \approx 14{,}3\%\),
— Для \(6\): \(\frac{4}{7} \cdot 100\% \approx 57{,}1429\% \approx 57{,}1\%\).
Проверим сумму процентов:
\[
14{,}3 + 14{,}3 + 14{,}3 + 57{,}1 = 100{,}0\%.
\]
Таблица относительных частот:
г)
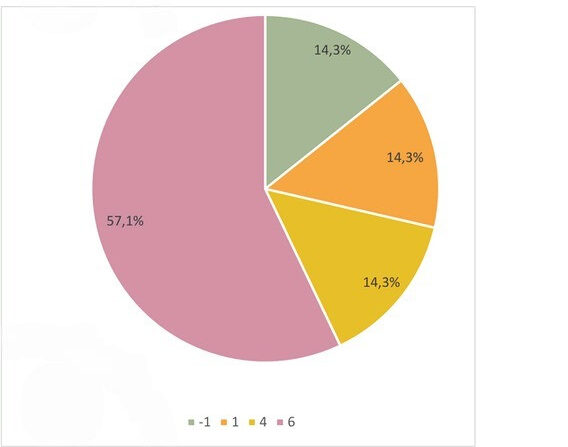
На основе полученных процентных частот строится круговая диаграмма . Каждому значению соответствует сектор, центральный угол которого пропорционален его частоте.
Такая диаграмма наглядно показывает, что значение 6 доминирует в выборке, составляя более половины всех наблюдений, в то время как остальные три значения встречаются с одинаковой (и значительно меньшей) частотой.
Ответ:
а) 6, 4, 1, 6, 6, –1, 6
б) абсолютные частоты: –1 → 1, 1 → 1, 4 → 1, 6 → 4
в) относительные частоты: –1 → 14,3%, 1 → 14,3%, 4 → 14,3%, 6 → 57,1%
г) круговая диаграмма построена в соответствии с указанными процентами и обозначениями