Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 36.18 Мордкович — Подробные Ответы
а) 2x² + xy = 0
x(2x + y) = 0
x = 0, y = –2x
б) xy – 5y = 0
y(x – 5) = 0
y = 0, x = 5
в) y² – 3xy = 0
y(y – 3x) = 0
y = 0, y = 3x
г) 4x + xy = 0
x(4 + y) = 0
x = 0, y = –4
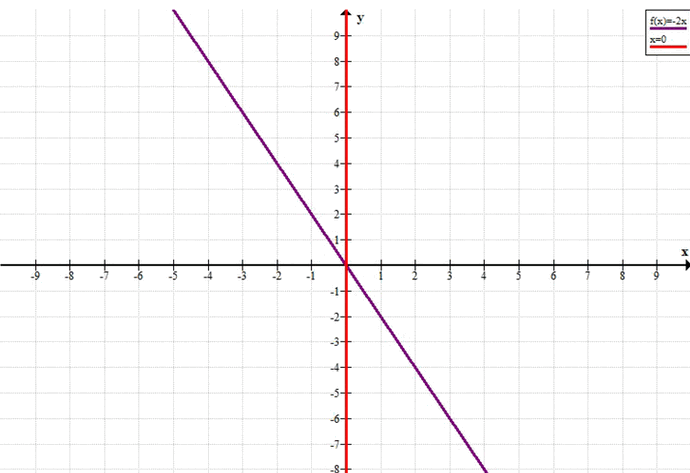
а) Уравнение \(2x^2 + xy = 0\)
Шаг 1: Вынесение общего множителя
Начнем с того, что мы можем вынести общий множитель \(x\):
\[
x(2x + y) = 0
\]
Шаг 2: Решение уравнения
Теперь у нас есть два возможных решения:
1. \(x = 0\)
2. \(2x + y = 0 > y = -2x\)
Это означает, что если \(x = 0\), то \(y\) может принимать любое значение. Если \(x\) не равен нулю, то \(y\) будет равно \(-2x\).
Графическое представление
— График \(y = -2x\) — это прямая линия с наклоном \(-2\), проходящая через начало координат.
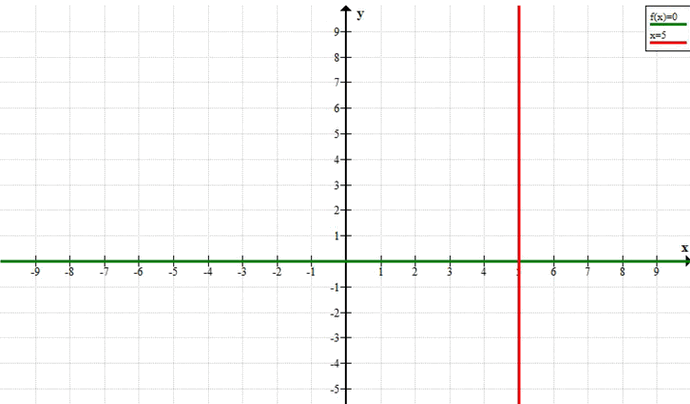
б) Уравнение \(xy — 5y = 0\)
Шаг 1: Вынесение общего множителя
В этом уравнении также можем вынести \(y\):
\[
y(x — 5) = 0
\]
Шаг 2: Решение уравнения
Теперь у нас есть два возможных решения:
1. \(y = 0\)
2. \(x — 5 = 0 > x = 5\)
Это означает, что если \(y = 0\), то \(x\) может принимать любое значение. Если \(y\) не равен нулю, то \(x\) будет равно \(5\).
Графическое представление
— График \(y = 0\) — это горизонтальная прямая на оси \(x\).
— График \(x = 5\) — это вертикальная прямая на оси \(y\).
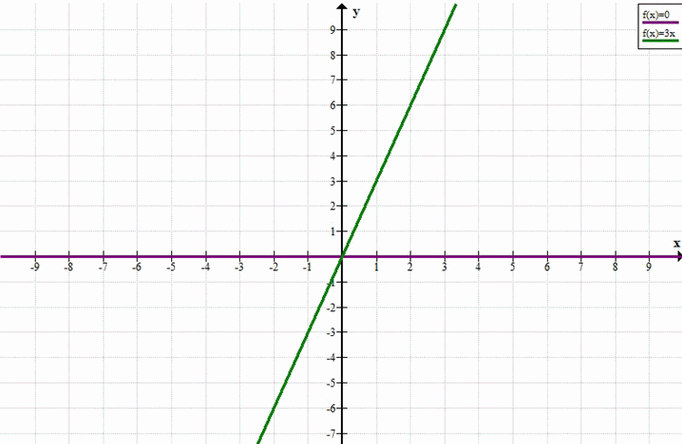
в) Уравнение \(y^2 — 3xy = 0\)
Шаг 1: Вынесение общего множителя
В этом уравнении можем вынести \(y\):
\[
y(y — 3x) = 0
\]
Шаг 2: Решение уравнения
Теперь у нас есть два возможных решения:
1. \(y = 0\)
2. \(y — 3x = 0 > y = 3x\)
Это означает, что если \(y = 0\), то \(x\) может принимать любое значение. Если \(y\) не равен нулю, то \(y\) будет равно \(3x\).
Графическое представление
— График \(y = 0\) — это горизонтальная прямая на оси \(x\).
— График \(y = 3x\) — это прямая линия с наклоном \(3\), проходящая через начало координат.
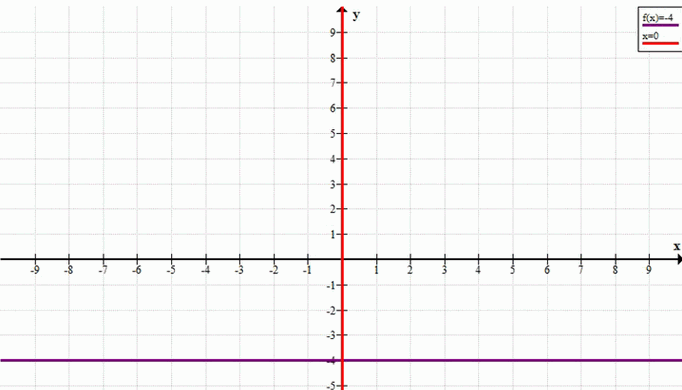
г) Уравнение \(4x + xy = 0\)
Шаг 1: Вынесение общего множителя
В этом уравнении можем вынести \(x\):
\[
x(4 + y) = 0
\]
Шаг 2: Решение уравнения
Теперь у нас есть два возможных решения:
1. \(x = 0\)
2. \(4 + y = 0 > y = -4\)
Это означает, что если \(x = 0\), то \(y\) может принимать любое значение. Если \(y\) не равен \(-4\), то \(x\) будет равно \(0\).
Графическое представление
— График \(x = 0\) — это вертикальная прямая на оси \(y\).
— График \(y = -4\) — это горизонтальная прямая на оси \(y\).
Общий вывод
Мы рассмотрели каждое уравнение, выделили корни и описали, как они могут быть визуализированы на графиках. Вот краткое резюме:
1. Уравнение \(2x^2 + xy = 0\):
— Решения: \(x = 0\) и \(y = -2x\)
— График: Прямая \(y = -2x\)
2. Уравнение \(xy — 5y = 0\):
— Решения: \(y = 0\) и \(x = 5\)
— Графики: Горизонтальная прямая \(y = 0\) и вертикальная прямая \(x = 5\)
3. Уравнение \(y^2 — 3xy = 0\):
— Решения: \(y = 0\) и \(y = 3x\)
— Графики: Горизонтальная прямая \(y = 0\) и прямая \(y = 3x\)
4. Уравнение \(4x + xy = 0\):
— Решения: \(x = 0\) и \(y = -4\)
— Графики: Вертикальная прямая \(x = 0\) и горизонтальная прямая \(y = -4\)
Эти графики могут быть нарисованы для визуализации решений.