ГДЗ по Алгебре 7 Класс Номер 37.27 Мордкович — Подробные Ответы

Постройте график уравнения: а) 2×2 + 3ху + 6\(x = 0\); б) х2у + ху2 = 0; в) 2ху — 3у2 — 6\(у = 0\); г) 2х2у — ху2 = 0.

а)
\( 2x^2 + 3xy + 6x = 0 \)

\( x(2x + 3y + 6) = 0 \)

\( x = 0 \) или \( 2x + 3y + 6 = 0 \)

\( 3y = -2x — 6 \)

\( y = -\frac{2}{3}x — 2 \)

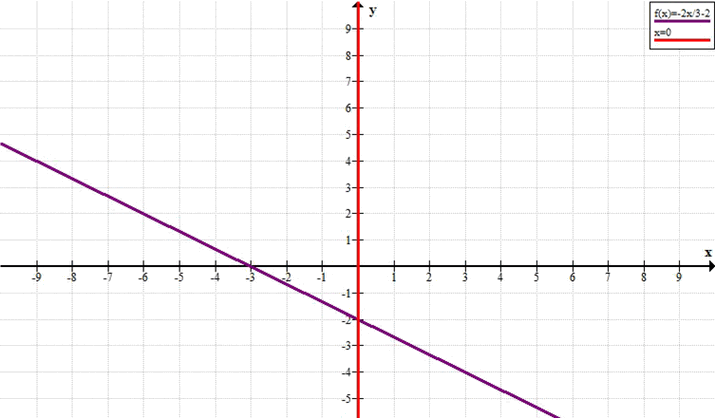
Прямая \( x=0 \) и прямая \( y = -\frac{2}{3}x — 2 \)

б)
\( x^2y + xy^2 = 0 \)

\( xy(x + y) = 0 \)

\( x = 0 \) или \( y = 0 \) или \( x + y = 0 \)

\( y = -x \)

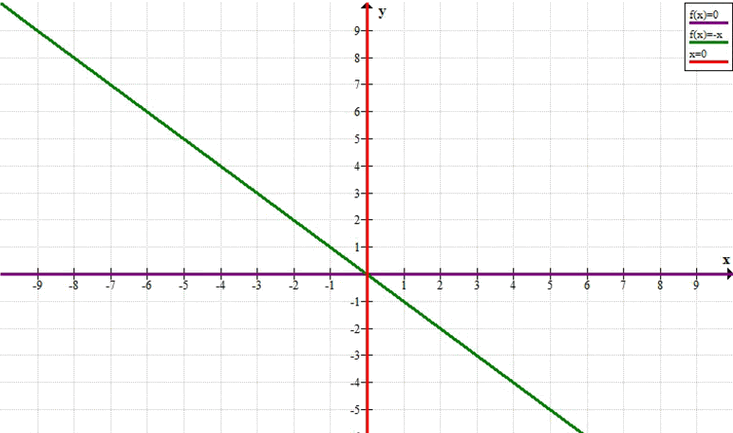
Прямые \( x=0 \), \( y=0 \) и \( y = -x \)

в)
\( 2xy — 3y^2 — 6y = 0 \)

\( y(2x — 3y — 6) = 0 \)

\( y = 0 \) или \( 2x — 3y — 6 = 0 \)

\( 3y = 2x — 6 \)

\( y = \frac{2}{3}x — 2 \)

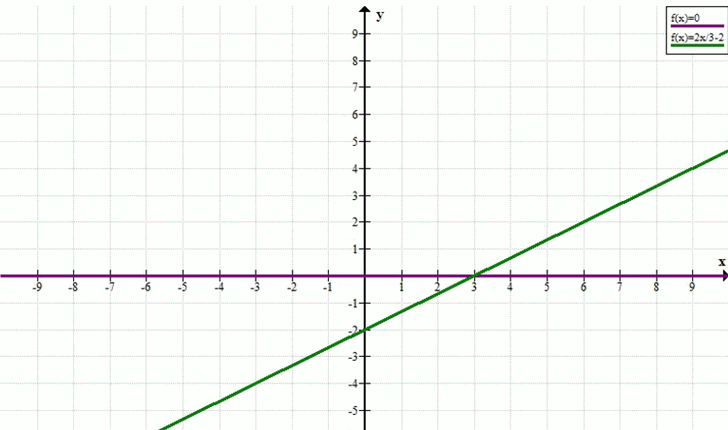
Прямая \( y=0 \) и прямая \( y = \frac{2}{3}x — 2 \)

г)
\( 2x^2y — xy^2 = 0 \)

\( xy(2x — y) = 0 \)

\( x = 0 \) или \( y = 0 \) или \( 2x — y = 0 \)

\( y = 2x \)

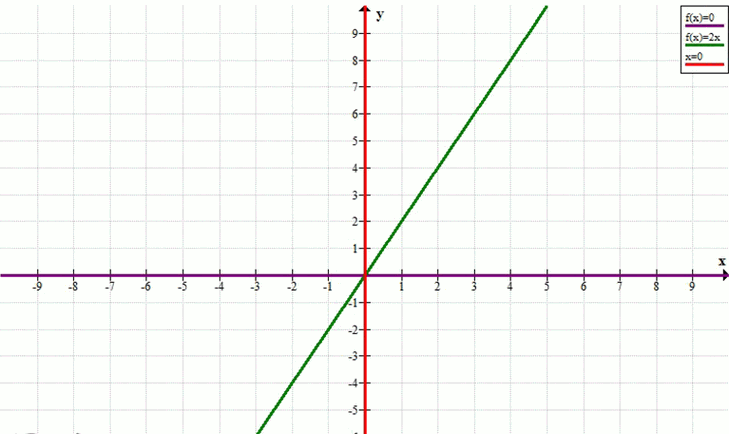
Прямые \( x=0 \), \( y=0 \) и \( y = 2x \)

Условие: Построить графики уравнений:

а)
\(2x^2 + 3xy + 6x = 0\);

б)
\(x^2y + xy^2 = 0\);

в)
\(2xy — 3y^2 — 6y = 0\);

г)
\(2x^2y — xy^2 = 0\).

Решение:

а)
\(2x^2 + 3xy + 6x = 0\)
\(x(2x + 3y + 6) = 0\)
— вынесение общего множителя
\(x = 0\) или \(2x + 3y + 6 = 0\)
— произведение равно нулю
График состоит из двух прямых: оси \(y\)
(\(x=0\)) и прямой \(2x + 3y + 6 = 0\).

б)
\(x^2y + xy^2 = 0\)
\(xy(x + y) = 0\)
— вынесение общего множителя
\(x = 0\) или \(y = 0\) или \(x + y = 0\)
— произведение равно нулю
График состоит из трех прямых: оси \(y\)
(\(x=0\)), оси \(x\)
(\(y=0\)) и прямой \(y = -x\).

в)
\(2xy — 3y^2 — 6y = 0\)
\(y(2x — 3y — 6) = 0\)
— вынесение общего множителя
\(y = 0\) или \(2x — 3y — 6 = 0\)
— произведение равно нулю
График состоит из двух прямых: оси \(x\)
(\(y=0\)) и прямой \(2x — 3y — 6 = 0\).

г)
\(2x^2y — xy^2 = 0\)
\(xy(2x — y) = 0\)
— вынесение общего множителя
\(x = 0\) или \(y = 0\) или \(2x — y = 0\) — произведение равно нулю
График состоит из трех прямых: оси \(y\)
(\(x=0\)), оси \(x\)
(\(y=0\)) и прямой \(y = 2x\).

Графики состоят из прямых линий, как описано в решении для каждого пункта.