Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 39.38 Мордкович — Подробные Ответы
\(а) (x + 1)^2 — у^2 = 0\); \(б) (х — 3)^2 — (у + 2)^2 = 0\); \(в) х^2 — (у — 2)^2 = 0\); \(г) (х + 4)^2 — (у — 1)^2 = 0\).
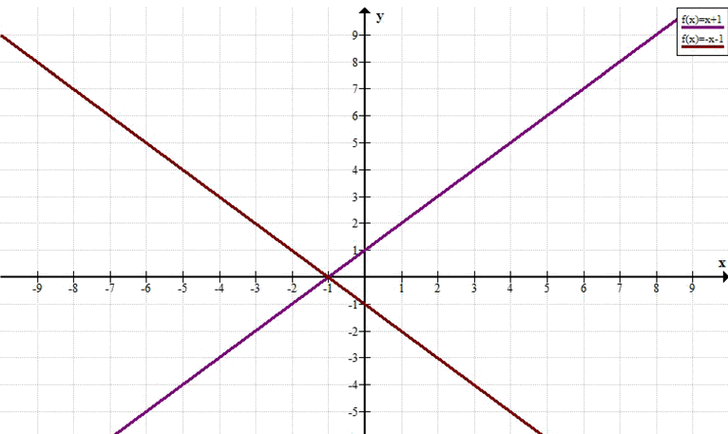
а)\( (x + 1)^2 — y^2 = 0 \)
\[
(x + 1 — y)(x + 1 + y) = 0
\]
\[
\Rightarrow \quad y = x + 1 \quad \text{или} \quad y = -x — 1.
\]
б) \( (x — 3)^2 — (y + 2)^2 = 0 \)
\[
(x — 3 — y — 2)(x — 3 + y + 2) = 0
\]
\[
(x — y — 5)(x + y — 1) = 0
\]
\[
\Rightarrow \quad y = x — 5 \quad \text{или} \quad y = -x + 1.
\]
в) \( x^2 — (y — 2)^2 = 0 \)
\[
(x — (y — 2))(x + (y — 2)) = 0
\]
\[
(x — y + 2)(x + y — 2) = 0
\]
\[
\Rightarrow \quad y = x + 2 \quad \text{или} \quad y = -x + 2.
\]
г) \( (x + 4)^2 — (y — 1)^2 = 0 \)
\[
(x + 4 — y + 1)(x + 4 + y — 1) = 0
\]
\[
(x — y + 5)(x + y + 3) = 0
\]
\[
\Rightarrow \quad y = x + 5 \quad \text{или} \quad y = -x — 3.
\]
а)\( (x + 1)^2 — y^2 = 0 \)
Левая часть — разность квадратов:
\[
A^2 — B^2 = (A — B)(A + B), \quad \text{где } A = x + 1,\; B = y.
\]
Применяем формулу:
\[
(x + 1)^2 — y^2 = \big[(x + 1) — y\big]\big[(x + 1) + y\big] = (x — y + 1)(x + y + 1).
\]
Уравнение принимает вид:
\[
(x — y + 1)(x + y + 1) = 0.
\]
Произведение равно нулю, если хотя бы один множитель равен нулю:
— \( x — y + 1 = 0 \;\Rightarrow\; y = x + 1 \);
— \( x + y + 1 = 0 \;\Rightarrow\; y = -x — 1 \).
Решение: объединение двух прямых \( y = x + 1 \) и \( y = -x — 1 \).
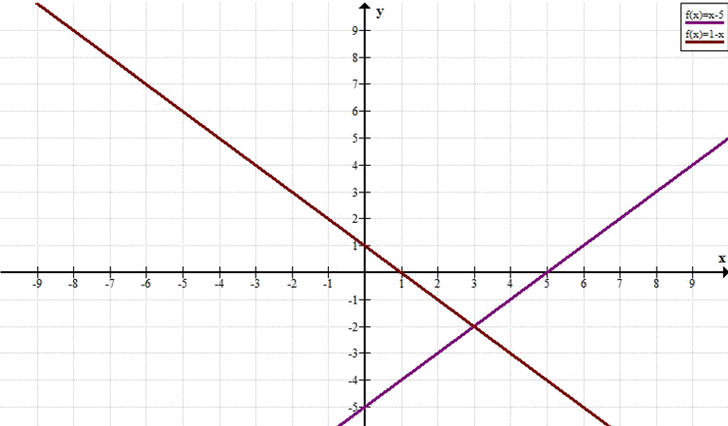
б) \( (x — 3)^2 — (y + 2)^2 = 0 \)
Это разность квадратов с \( A = x — 3 \), \( B = y + 2 \):
\[
(x — 3)^2 — (y + 2)^2 = \big[(x — 3) — (y + 2)\big]\big[(x — 3) + (y + 2)\big].
\]
Упрощаем множители:
— Первый: \( x — 3 — y — 2 = x — y — 5 \);
— Второй: \( x — 3 + y + 2 = x + y — 1 \).
Получаем:
\[
(x — y — 5)(x + y — 1) = 0.
\]
Приравниваем каждый множитель к нулю:
— \( x — y — 5 = 0 \;\Rightarrow\; y = x — 5 \);
— \( x + y — 1 = 0 \;\Rightarrow\; y = -x + 1 \).
Решение: две прямые \( y = x — 5 \) и \( y = -x + 1 \).
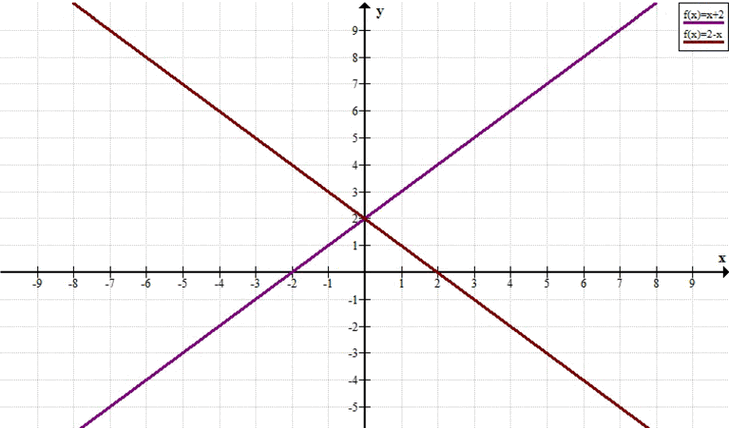
в) \( x^2 — (y — 2)^2 = 0 \)
Здесь \( A = x \), \( B = y — 2 \). Применяем формулу:
\[
x^2 — (y — 2)^2 = \big[x — (y — 2)\big]\big[x + (y — 2)\big] = (x — y + 2)(x + y — 2).
\]
Уравнение:
\[
(x — y + 2)(x + y — 2) = 0.
\]
Решаем:
— \( x — y + 2 = 0 \;\Rightarrow\; y = x + 2 \);
— \( x + y — 2 = 0 \;\Rightarrow\; y = -x + 2 \).
Решение: прямые \( y = x + 2 \) и \( y = -x + 2 \).
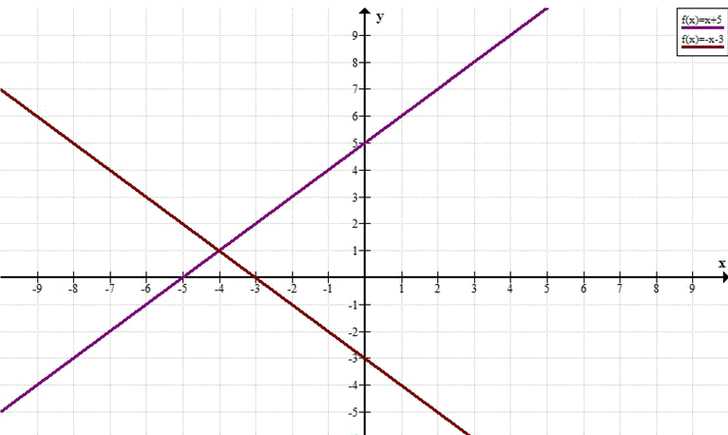
г) \( (x + 4)^2 — (y — 1)^2 = 0 \)
Положим \( A = x + 4 \), \( B = y — 1 \). Тогда:
\[
(x + 4)^2 — (y — 1)^2 = \big[(x + 4) — (y — 1)\big]\big[(x + 4) + (y — 1)\big].
\]
Упрощаем:
— Первый множитель: \( x + 4 — y + 1 = x — y + 5 \);
— Второй: \( x + 4 + y — 1 = x + y + 3 \).
Получаем:
\[
(x — y + 5)(x + y + 3) = 0.
\]
Приравниваем к нулю:
— \( x — y + 5 = 0 \;\Rightarrow\; y = x + 5 \);
— \( x + y + 3 = 0 \;\Rightarrow\; y = -x — 3 \).
Решение: прямые \( y = x + 5 \) и \( y = -x — 3 \).