ГДЗ по Алгебре 7 Класс Номер 40.27 Мордкович — Подробные Ответы

Постройте график уравнения:

а) \( x^2 — 6xy + 8y^2 = 0 \)
б) \( 2x^2 + 5xy + 2y^2 = 0 \)
в) \( x^2 + xy — 2y^2 = 0 \)
г) \( 3x^2 — 10xy + 3y^2 = 0 \)

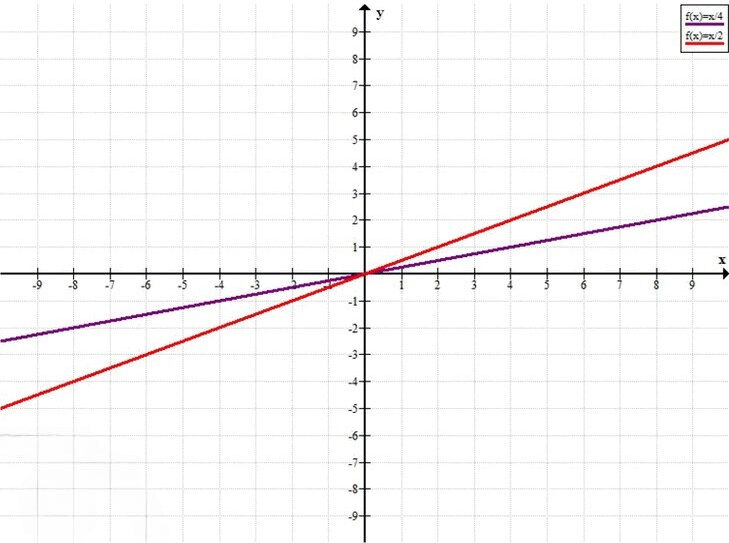
а)
\[
x^2 — 6xy + 8y^2 = 0
\]

\[
x^2 — 6xy + 9y^2 — y^2 = 0
\]

\[
(x — 3y)^2 — y^2 = 0
\]

\[
(x — 3y — y)(x — 3y + y) = 0
\]

\[
(x — 4y)(x — 2y) = 0
\]

\[
x = 4y \quad \text{или} \quad x = 2y
\]

\[
y = \frac{x}{4} \quad \text{или} \quad y = \frac{x}{2}
\]

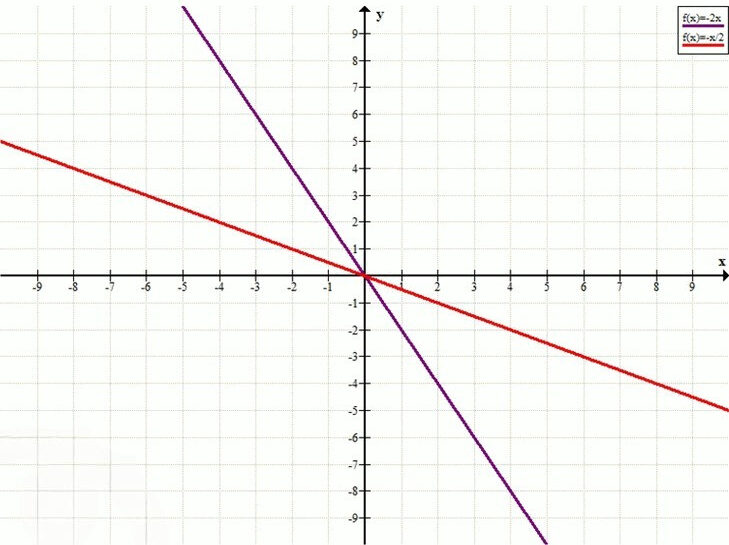
б)

\[
2x^2 + 5xy + 2y^2 = 0
\]

\[
2x^2 + 4xy + xy + 2y^2 = 0
\]

\[
2x(x + 2y) + y(x + 2y) = 0
\]

\[
(x + 2y)(2x + y) = 0
\]

\[
x + 2y = 0 \quad \text{или} \quad 2x + y = 0
\]

\[
y = -\frac{x}{2} \quad \text{или} \quad y = -2x
\]

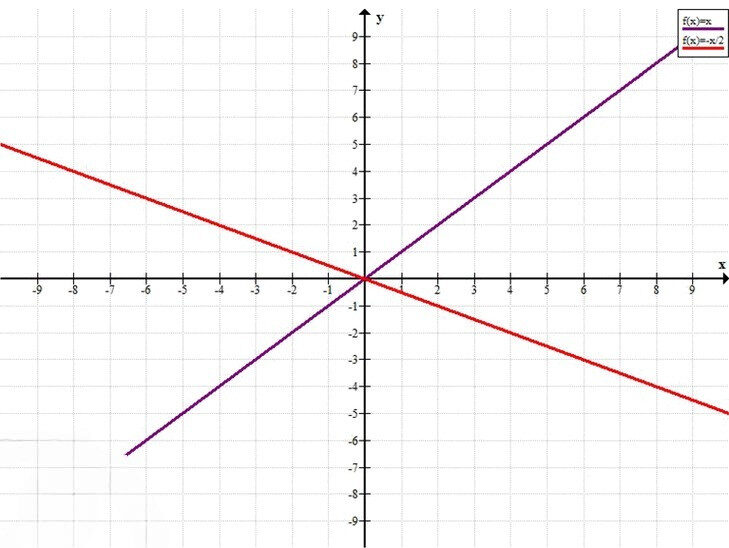
в)

\[
x^2 + xy — 2y^2 = 0
\]

\[
x^2 + 2xy — xy — 2y^2 = 0
\]

\[
x(x + 2y) — y(x + 2y) = 0
\]

\[
(x + 2y)(x — y) = 0
\]

\[
x + 2y = 0 \quad \text{или} \quad x — y = 0
\]

\[
y = -\frac{x}{2} \quad \text{или} \quad y = x
\]

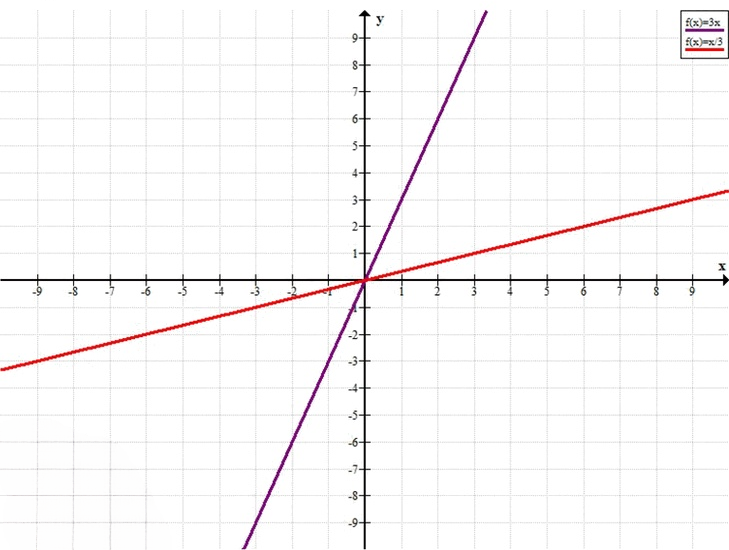
г)

\[
3x^2 — 10xy + 3y^2 = 0
\]

\[
3x^2 — 9xy — xy + 3y^2 = 0
\]

\[
3x(x — 3y) — y(x — 3y) = 0
\]

\[
(x — 3y)(3x — y) = 0
\]

\[
x — 3y = 0 \quad \text{или} \quad 3x — y = 0
\]

\[
y = \frac{x}{3} \quad \text{или} \quad y = 3x
\]

а)
дано уравнение:
\[
x^2 — 6xy + 8y^2 = 0.
\]

поскольку стандартная группировка неочевидна, применим метод выделения полного квадрата.
заметим, что \(x^2 — 6xy + 9y^2 = (x — 3y)^2\).
чтобы получить это выражение, прибавим и вычтем \(y^2\):
\[
x^2 — 6xy + 8y^2 = (x^2 — 6xy + 9y^2) — y^2 = (x — 3y)^2 — y^2.
\]

получена разность квадратов:
\[
(x — 3y)^2 — y^2 = \big((x — 3y) — y\big)\big((x — 3y) + y\big) = (x — 4y)(x — 2y).
\]

следовательно, уравнение принимает вид:
\[
(x — 4y)(x — 2y) = 0.
\]

произведение равно нулю, если хотя бы один из множителей равен нулю:
\[
x — 4y = 0 \quad \text{или} \quad x — 2y = 0.
\]

решим каждое уравнение относительно \(y\):
\[
x = 4y \;\Rightarrow\; y = \frac{x}{4}, \qquad
x = 2y \;\Rightarrow\; y = \frac{x}{2}.
\]

б)
дано уравнение:
\[
2x^2 + 5xy + 2y^2 = 0.
\]

разложим средний член \(5xy\) на сумму \(4xy + xy\), чтобы можно было сгруппировать:
\[
2x^2 + 4xy + xy + 2y^2 = 0.
\]

сгруппируем первые два и последние два слагаемых:
\[
(2x^2 + 4xy) + (xy + 2y^2) = 0.
\]

из первой группы выносим \(2x\), из второй — \(y\):
\[
2x(x + 2y) + y(x + 2y) = 0.
\]

общий множитель \((x + 2y)\) выносим за скобки:
\[
(x + 2y)(2x + y) = 0.
\]

приравниваем каждый множитель к нулю:
\[
x + 2y = 0 \quad \text{или} \quad 2x + y = 0.
\]

выразим \(y\) через \(x\):
\[
x = -2y \;\Rightarrow\; y = -\frac{x}{2}, \qquad
y = -2x.
\]

в)
дано уравнение:
\[
x^2 + xy — 2y^2 = 0.
\]

разложим средний член: \(xy = 2xy — xy\), тогда:
\[
x^2 + 2xy — xy — 2y^2 = 0.
\]

сгруппируем:
\[
(x^2 + 2xy) + (-xy — 2y^2) = 0.
\]

вынесем общие множители:
\[
x(x + 2y) — y(x + 2y) = 0.
\]

общий множитель \((x + 2y)\):
\[
(x + 2y)(x — y) = 0.
\]

приравниваем к нулю:
\[
x + 2y = 0 \quad \text{или} \quad x — y = 0.
\]

решаем относительно \(y\):
\[
y = -\frac{x}{2} \quad \text{или} \quad y = x.
\]

г)
дано уравнение:
\[
3x^2 — 10xy + 3y^2 = 0.
\]

разложим средний член \(-10xy\) как \(-9xy — xy\):
\[
3x^2 — 9xy — xy + 3y^2 = 0.
\]

сгруппируем:
\[
(3x^2 — 9xy) + (-xy + 3y^2) = 0.
\]

вынесем множители:
\[
3x(x — 3y) — y(x — 3y) = 0.
\]

общий множитель \((x — 3y)\):
\[
(x — 3y)(3x — y) = 0.
\]

приравниваем к нулю:
\[
x — 3y = 0 \quad \text{или} \quad 3x — y = 0.
\]

выразим \(y\):
\[
x = 3y \;\Rightarrow\; y = \frac{x}{3}, \qquad
y = 3x.
\]

ответ:
а) \(y = \frac{x}{4}\), \(y = \frac{x}{2}\)
б) \(y = -\frac{x}{2}\), \(y = -2x\)
в) \(y = -\frac{x}{2}\), \(y = x\)
г) \(y = \frac{x}{3}\), \(y = 3x\)