Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.13 Мордкович — Подробные Ответы
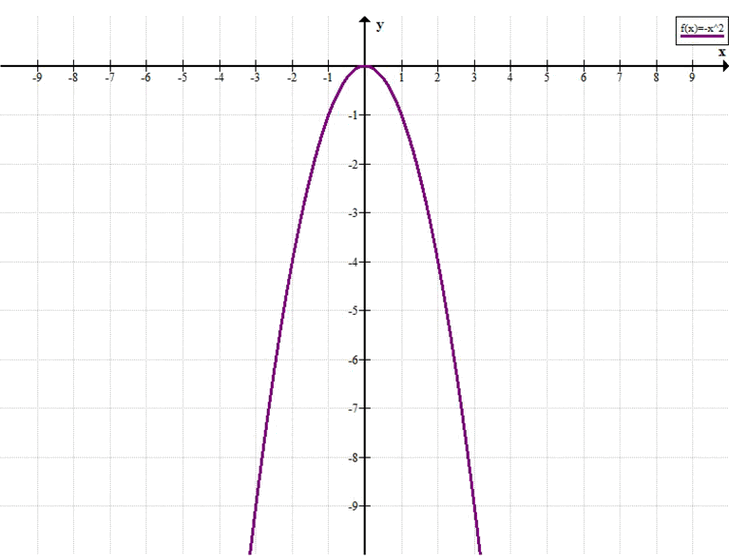
Постройте график функции \( y = -x^2 \). С помощью графика найдите:
а) значения функции при \( x = -1 \), \( x = 1 \)
б) значения аргумента при \( y = -1 \)
в) значения \( x \), если \( y < -1 \), \( y > -1 \)
г) значения \( y \), если \( -1 < x < 0 \)
Функция: \( y = -x^2 \)
а) Найдём значение функции при \( x = -1 \):
\[
y = -(-1)^2
\]
\[
y = -1
\]
Найдём значение функции при \( x = 1 \):
\[
y = -(1)^2
\]
\[
y = -1
\]
б) Найдём все значения \( x \), при которых \( y = -1 \):
\[
-x^2 = -1
\]
\[
x^2 = 1
\]
\[
x = \pm 1
\]
в) Определим, при каких \( x \) выполняется \( y < -1 \):
\[
-x^2 < -1
\]
\[
x^2 > 1
\]
\[
x < -1 \quad \text{или} \quad x > 1
\]
Определим, при каких \( x \) выполняется \( y > -1 \):
\[
-x^2 > -1
\]
\[
x^2 < 1
\]
\[
-1 < x < 1
\]
г) Рассмотрим промежуток \( -1 < x < 0 \). Поскольку функция \( y = -x^2 \) возрастает на этом интервале
(так как \( x \) отрицательный, а квадрат уменьшается при приближении к нулю), то:
\[
x \to -1^+ \quad \Rightarrow \quad y = -x^2 \to -1^-
\]
\[
x \to 0^- \quad \Rightarrow \quad y = -x^2 \to 0^-
\]
\[
\text{Следовательно, } y \in (-1; 0)
\]
\[
-1 < y < 0
\]
Функция: \( y = -x^2 \)
а) Найдём значение функции при \( x = -1 \). Подставим это значение в формулу:
\[
y = -(-1)^2
\]
\[
(-1)^2 = (-1) \cdot (-1) = 1
\]
\[
y = -1
\]
Теперь найдём значение функции при \( x = 1 \):
\[
y = -(1)^2
\]
\[
(1)^2 = 1 \cdot 1 = 1
\]
\[
y = -1
\]
б) Найдём все значения аргумента \( x \), при которых \( y = -1 \). Для этого решим уравнение:
\[
-x^2 = -1
\]
Умножим обе части уравнения на \(-1\), чтобы избавиться от знака минус:
\[
x^2 = 1
\]
Извлечём квадратный корень из обеих частей. Учтём, что уравнение \( x^2 = a \) при \( a > 0 \) имеет два решения:
\[
x = \sqrt{1} \quad \text{или} \quad x = -\sqrt{1}
\]
\[
x = 1 \quad \text{или} \quad x = -1
\]
\[
x = \pm 1
\]
в) Определим, при каких значениях \( x \) выполняется неравенство \( y < -1 \). Подставим выражение для \( y \):
\[
-x^2 < -1
\]
Умножим обе части неравенства на \(-1\). При умножении на отрицательное число знак неравенства меняется на противоположный:
\[
x^2 > 1
\]
Решим полученное неравенство. Выражение \( x^2 > 1 \) означает, что модуль \( x \) больше 1:
\[
x < -1 \quad \text{или} \quad x > 1
\]
Теперь определим, при каких \( x \) выполняется \( y > -1 \):
\[
-x^2 > -1
\]
Снова умножим обе части на \(-1\), меняя знак неравенства:
\[
x^2 < 1
\]
Это неравенство выполняется, когда \( x \) находится между \(-1\) и \(1\):
\[
-1 < x < 1
\]
г) Рассмотрим промежуток \( -1 < x < 0 \). На этом интервале переменная \( x \) отрицательна, но её модуль уменьшается при приближении к нулю.
Поскольку \( y = -x^2 \), а \( x^2 \) уменьшается от \(1\) до \(0\), то \( y \) возрастает от \(-1\) до \(0\).
Найдём предельные значения:
\[
\text{При } x \to -1^+ \text{ (справа от } -1\text{): } x^2 \to 1, \quad y = -x^2 \to -1
\]
\[
\text{При } x \to 0^- \text{ (слева от } 0\text{): } x^2 \to 0, \quad y = -x^2 \to 0
\]
Так как концы интервала не включены (\( -1 < x < 0 \)), значения \( y = -1 \) и \( y = 0 \) не достигаются. Следовательно:
\[
y \in (-1; 0)
\]
\[
-1 < y < 0
\]
Ответы:
а) При \( x = -1 \) и \( x = 1 \) имеем \( y = -1 \).
б) \( y = -1 \) при \( x = \pm 1 \).
в) \( y < -1 \) при \( x < -1 \) или \( x > 1 \); \( y > -1 \) при \( -1 < x < 1 \).
г) При \( -1 < x < 0 \) выполняется \( -1 < y < 0 \).