ГДЗ по Алгебре 7 Класс Номер 44.26 Мордкович — Подробные Ответы

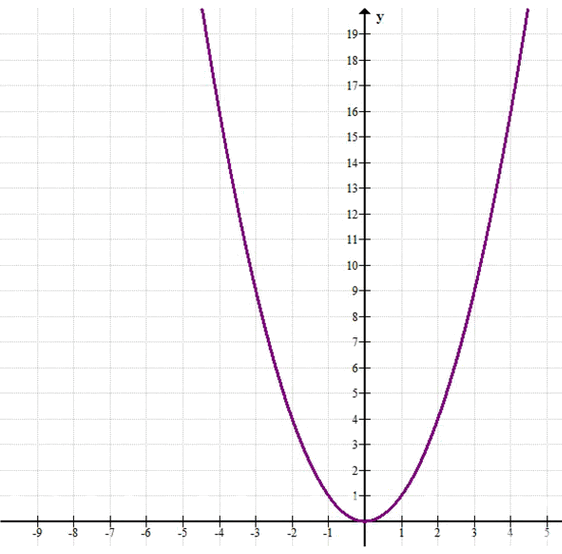
Постройте график функции \( y = x^2 \). С помощью графика найдите:

а) значения функции при значении аргумента, равном \(-4\); \(0\); \(2\);
б) значения аргумента, если значение функции равно \(1\); \(0\); \(9\);
в) наибольшее и наименьшее значения функции на отрезке \([-1; 2]\);
г) значения аргумента, при которых \(1 < y < 9\).

y = x²

а) x = –4, y = 16;
x = 0, y = 0;
x = 2, y = 4.

б) y = 1, x = ±1;
y = 0, x = 0;
y = 9, x = ±3.

в) [–1; 2]
y наим = 0, y наиб = 4.

г) 1 < y < 9, –3 < x < –1 и 1 < x < 3.

Условие: Постройте график функции \(у = х^2\). С помощью графика найдите:

а) значения функции при значении аргумента, равном -4; 0; 2;

б) значения аргумента, если значение функции равно 1; 0; 9;

в) наибольшее и наименьшее значения функции на отрезке [-1; 2]; г) значения аргумента, при которых \(1 < у < 9\).

Решение:
Построение графика функции \(у = х^2\):
Графиком функции \(у = х^2\) является парабола, ветви которой направлены вверх, а вершина находится в начале координат \((0; 0)\). Осью симметрии параболы является ось \(у\).

а) Найдем значения функции при заданных значениях аргумента:
При \(х = -4\):
\(у = (-4)^2\)
\(у = 16\)
При \(х = 0\):
\(у = (0)^2\)
\(у = 0\)
При \(х = 2\):
\(у = (2)^2\)
\(у = 4\)

б) Найдем значения аргумента при заданных значениях функции:
При \(у = 1\):
\(х^2 = 1\)
\(х = \pm\sqrt{1}\)
\(х = \pm 1\)
При \(у = 0\):
\(х^2 = 0\)
\(х = 0\)
При \(у = 9\):
\(х^2 = 9\)
\(х = \pm\sqrt{9}\)
\(х = \pm 3\)

в) Найдем наибольшее и наименьшее значения функции на отрезке \([-1; 2]\):
Функция \(у = х^2\) является параболой с вершиной в точке \((0; 0)\).
На отрезке \([-1; 2]\) наименьшее значение функции достигается в вершине параболы, так как \(0 \in [-1; 2]\).
Наименьшее значение:
\(у_{min} = (0)^2 = 0\)
Наибольшее значение функции на отрезке достигается на одном из его концов, который наиболее удален от оси симметрии \(х = 0\).
Сравним значения функции на концах отрезка:
При \(х = -1\): \(у = (-1)^2 = 1\)
При \(х = 2\): \(у = (2)^2 = 4\)
Наибольшее значение:
\(у_{max} = 4\)

г) Найдем значения аргумента, при которых \(1 < у < 9\):
Необходимо решить двойное неравенство \(1 < х^2 < 9\).
Это эквивалентно системе неравенств:
\(х^2 > 1\) и \(х^2 < 9\)
Решим первое неравенство \(х^2 > 1\):
\(х^2 — 1 > 0\)
\((х — 1)(х + 1) > 0\)
Решением является \(х \in (-\infty; -1) \cup (1; +\infty)\).
Решим второе неравенство \(х^2 < 9\):
\(х^2 — 9 < 0\)
\((х — 3)(х + 3) < 0\)
Решением является \(х \in (-3; 3)\).
Найдем пересечение решений обоих неравенств:
\(х \in ((-\infty; -1) \cup (1; +\infty)) \cap (-3; 3)\)
Это дает:
\(х \in (-3; -1) \cup (1; 3)\)

Ответ:
а) При \(х = -4\), \(у = 16\); при \(х = 0\), \(у = 0\); при \(х = 2\), \(у = 4\).
б) При \(у = 1\), \(х = \pm 1\); при \(у = 0\), \(х = 0\); при \(у = 9\), \(х = \pm 3\).
в) Наименьшее значение функции на отрезке \([-1; 2]\) равно 0, наибольшее значение равно 4.
г) Значения аргумента, при которых \(1 < у < 9\), находятся в интервалах \(х \in (-3; -1) \cup (1; 3)\).