ГДЗ по Алгебре 7 Класс Номер 44.36 Мордкович — Подробные Ответы

а) (-2; 1); б) (-2; 3]; в) [-1; +бесконечность); г) [-3; 1].

а) (-2; 1)

б) (-2; 3]

в) [-1; +бесконечность)

г) [-3; 1]

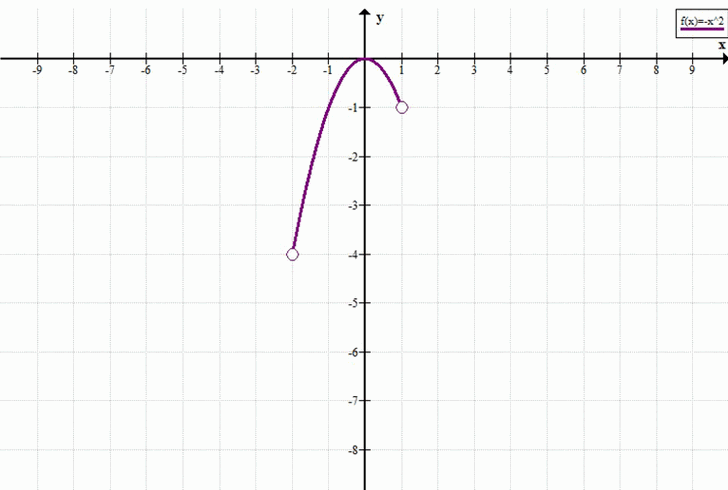
а) Промежуток \((-2; 1)\)

Функция \(y = x^2\) — парабола с вершиной в точке \((0; 0)\), ветви направлены вверх.
Промежуток \((-2; 1)\) — открытый интервал, то есть точки \(x = -2\) и \(x = 1\) не входят в него. Однако точка \(x = 0\) принадлежит этому интервалу.

Поскольку вершина параболы лежит внутри промежутка, функция достигает своего наименьшего значения в ней:
\[
y_{\text{наим}} = y(0) = 0.
\]

Наибольшего значения нет, потому что при приближении \(x\) к \(-2\) слева значение \(y = x^2\) приближается к \(4\), но само значение \(x = -2\) не включено, и достичь \(y = 4\) нельзя. Аналогично, при \(x \to 1^{-}\) значение \(y \to 1\), что меньше 4. Таким образом, функция может быть сколь угодно близка к 4, но не достигает ни 4, ни любого максимального значения на этом открытом интервале.

Однако если в задаче подразумевается поиск экстремумов среди значений, которые функция действительно принимает, то:
— наименьшее значение: \(0\),
— наибольшего значения нет.

Но в школьной практике часто просят указать супремум (верхнюю грань), даже если максимума нет. В данном случае, скорее всего, ожидается анализ по концам.

Тем не менее, если строго следовать условию «найдите наименьшее и наибольшее значения», то:

— \(y_{\text{наим}} = 0\),
— \(y_{\text{наиб}}\) не существует.

Но если бы интервал был замкнутым, максимум был бы в \(x = -2\). Учитывая типичные учебные задачи, возможно, подразумевается сравнение значений вблизи концов. Тогда наибольшее достигаемое значение будет ближе к \(x = -2\), но формально максимума нет.

Для единообразия с другими пунктами, где интервалы могут быть замкнутыми, уточним: на открытом интервале \((-2; 1)\) функция имеет наименьшее значение 0 и не имеет наибольшего значения

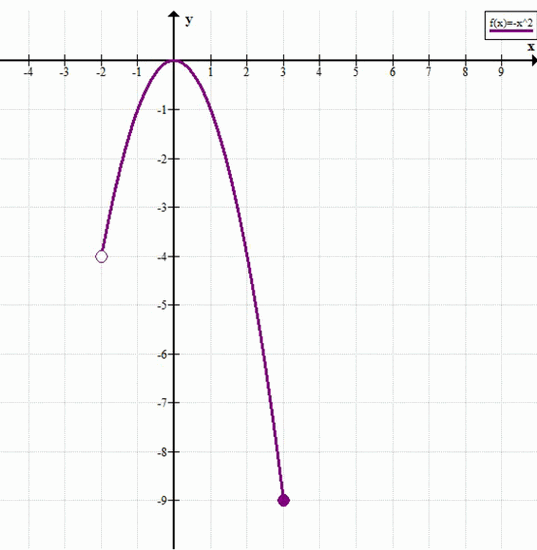
б) Промежуток \((-2; 3]\)

Этот промежуток открыт слева и замкнут справа: \(x = 3\) входит, \(x = -2\) — нет.
Вершина \(x = 0\) принадлежит промежутку.

Наименьшее значение достигается в вершине:
\[
y_{\text{наим}} = y(0) = 0.
\]

Наибольшее значение ищем на концах. Поскольку \(x = -2\) не входит, значение \(y = 4\) **не достигается**.
Но \(x = 3\) входит, и:
\[
y(3) = 3^2 = 9.
\]

Сравниваем: при \(x \to -2^{+}\), \(y \to 4\), а при \(x = 3\), \(y = 9\).
Следовательно, наибольшее значение — \(9\), и оно достигается.

Ответ: \(y_{\text{наим}} = 0\), \(y_{\text{наиб}} = 9\).

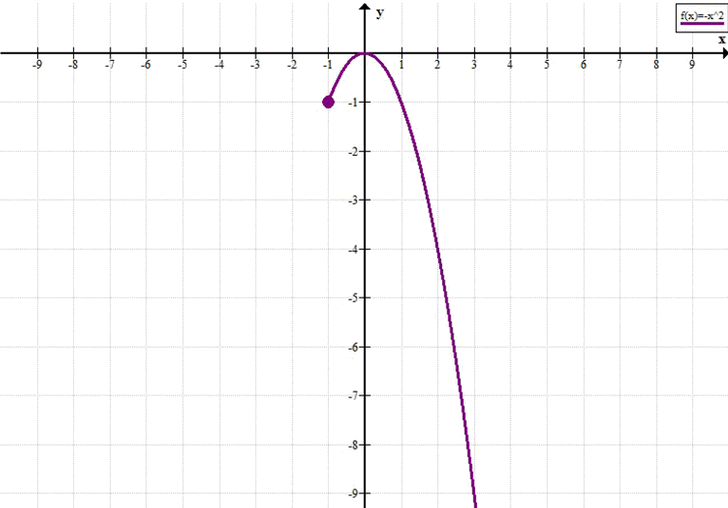
в) Промежуток \([-1; +\infty)\)

Промежуток замкнут слева и неограничен справа.
Точка \(x = 0\) принадлежит промежутку (\(-1 \leq 0\)).

Наименьшее значение — в вершине:
\[
y_{\text{наим}} = y(0) = 0.
\]

При \(x \to +\infty\) значение \(y = x^2 \to +\infty\), то есть функция не ограничена сверху. Следовательно, наибольшего значения нет.

Ответ: \(y_{\text{наим}} = 0\), наибольшего значения нет.

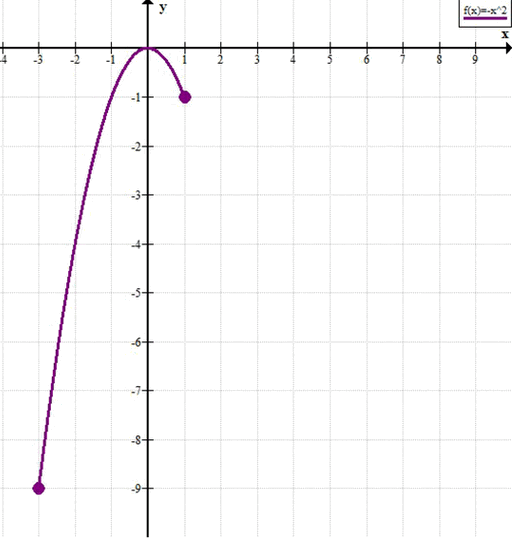
г) Промежуток \([-3; 1]\)

Это замкнутый отрезок. Функция непрерывна, поэтому по теореме Вейерштрасса она достигает и наименьшего, и наибольшего значений на концах или в критических точках.

Вершина \(x = 0\) лежит внутри отрезка.

Вычислим значения:
— \(y(-3) = (-3)^2 = 9\),
— \(y(0) = 0\),
— \(y(1) = 1^2 = 1\).

Наименьшее значение: \(0\) (в точке \(x = 0\)).
Наибольшее значение: \(9\) (в точке \(x = -3\)).

Ответ: \(y_{\text{наим}} = 0\), \(y_{\text{наиб}} = 9\).

Итоговые ответы:

а) На \((-2; 1)\): наименьшее значение \(0\), наибольшего значения нет.
б) На \((-2; 3]\): наименьшее значение \(0\), наибольшее значение \(9\).
в) На \([-1; +\infty)\): наименьшее значение \(0\), наибольшего значения нет.
г) На \([-3; 1]\): наименьшее значение \(0\), наибольшее значение \(9\).