Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.41 Мордкович — Подробные Ответы
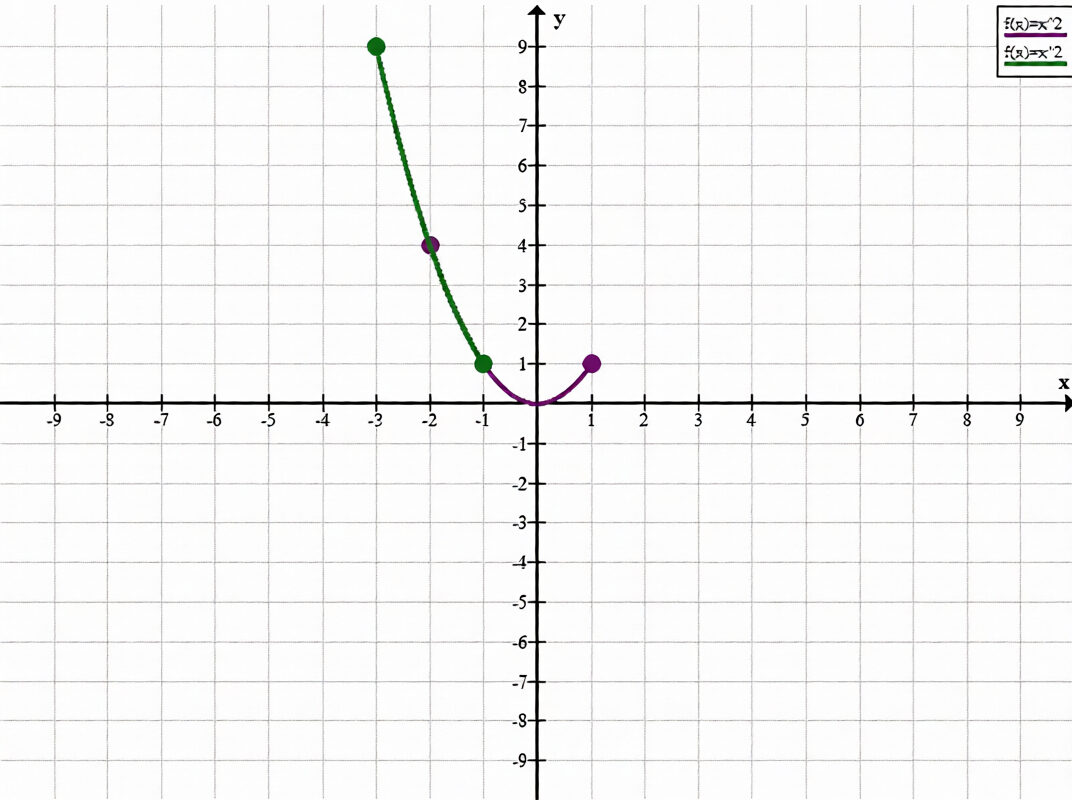
Пусть \(A\) — наименьшее значение функции \(y = x^2\) на отрезке \([-2; 1]\), а \(B\) — наибольшее значение той же функции на отрезке \([-3; -1]\). что больше: \(A\) или \(B\)?
y = x², [−2; 1], Aнаим = 0.
y = x₂, [−3; −1], Bнаиб = 9.
B > A
рассмотрим функцию \(y = x^2\). это парабола с вершиной в точке \((0; 0)\), ветви направлены вверх. на любом отрезке, содержащем ноль, наименьшее значение равно \(0\).
найдём \(A\) — наименьшее значение на отрезке \([-2; 1]\):
отрезок содержит \(x = 0\), поэтому:
\[
A = y(0) = 0^2 = 0
\]
найдём \(B\) — наибольшее значение на отрезке \([-3; -1]\):
этот отрезок лежит слева от нуля, функция убывает при \(x < 0\), значит наибольшее значение достигается при наименьшем \(x\), то есть при \(x = -3\):
\[
B = y(-3) = (-3)^2 = 9
\]
сравниваем:
\[
A = 0, \quad B = 9 \Rightarrow A < B
\]
итоговые ответы:
\(A = 0\), \(B = 9\), следовательно, \(A < B\).