Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.45 Мордкович — Подробные Ответы
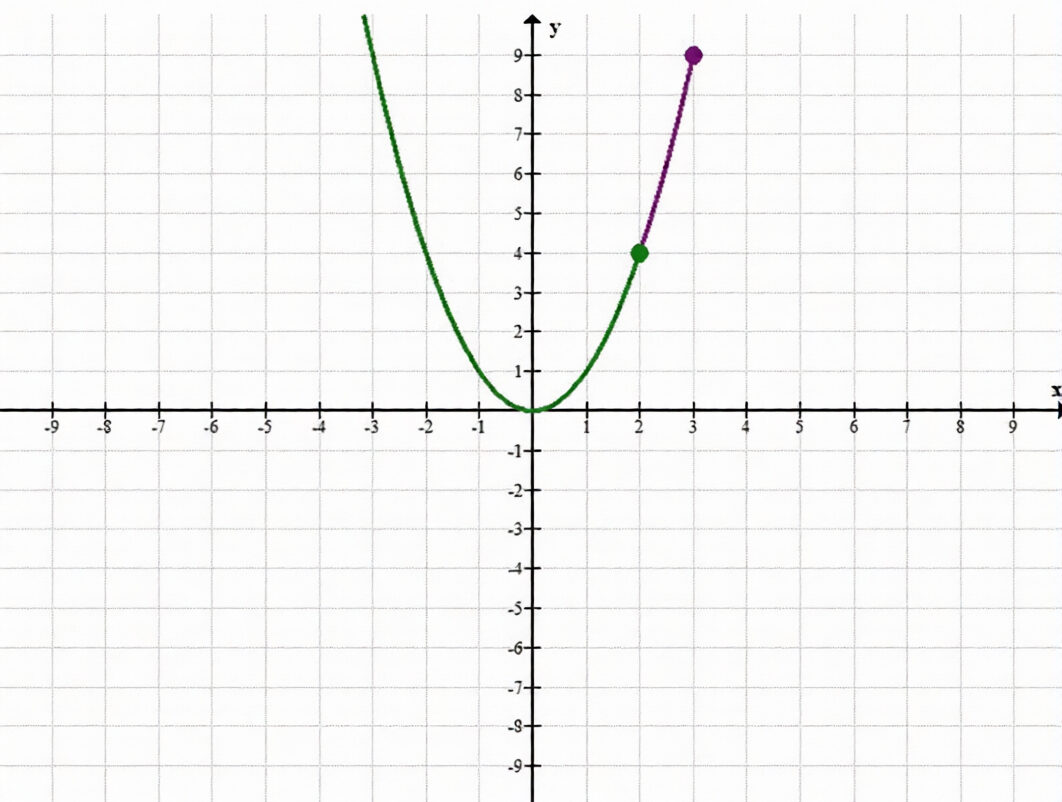
Пусть \(P\) — наименьшее значение функции \(y = x^2\) на луче \((-\infty; 3]\), а \(Q\) — наименьшее значение той же функции на луче \((-\infty; 2]\). что больше: \(P\) или \(Q\)? сделайте графическую иллюстрацию.
рассматривается функция
\[
y = x^2
\]
на двух полубесконечных отрезках:
— первый: \(x \in (-\infty; 3]\) — обозначим наименьшее значение как \(P_{\text{наим}}\);
— второй: \(x \in (-\infty; 2]\) — обозначим наименьшее значение как \(Q_{\text{наим}}\).
требуется найти эти значения и сравнить их.
1. Анализ функции \(y = x^2\) на промежутке \((-\infty; 3]\).
функция \(y = x^2\) имеет вершину в точке \((0; 0)\), где достигает своего глобального минимума.
поскольку \(0 \in (-\infty; 3]\) (то есть ноль принадлежит этому промежутку), то наименьшее значение функции на всём промежутке достигается именно в этой точке:
\[
y(0) = 0^2 = 0.
\]
при этом при \(x \to -\infty\) значение функции стремится к \(+\infty\), а при \(x = 3\) — равно \(9\), но это не влияет на минимум, так как он уже найден в нуле.
следовательно:
\[
P_{\text{наим}} = 0.
\]
2. Анализ функции \(y = x^2\) на промежутке \((-\infty; 2]\).
аналогично, точка \(x = 0\) принадлежит этому промежутку, так как \(0 < 2\).
значит, минимальное значение функции снова достигается в нуле:
\[
y(0) = 0^2 = 0.
\]
при \(x = 2\) значение функции равно \(4\), а при \(x \to -\infty\) — стремится к бесконечности, но это не меняет положения минимума.
поэтому:
\[
Q_{\text{наим}} = 0.
\]
3. Сравнение значений.
получаем:
\[
P_{\text{наим}} = 0, \quad Q_{\text{наим}} = 0 \quad \Rightarrow \quad P = Q.
\]
это равенство объясняется тем, что оба промежутка содержат точку \(x = 0\), где функция \(y = x^2\) достигает своего абсолютного минимума. даже если один из промежутков «короче» другого, это не влияет на значение минимума — оно определяется только наличием точки \(x = 0\).
ответ:
\(P_{\text{наим}} = 0\), \(Q_{\text{наим}} = 0\), \(P = Q\).