Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.46 Мордкович — Подробные Ответы
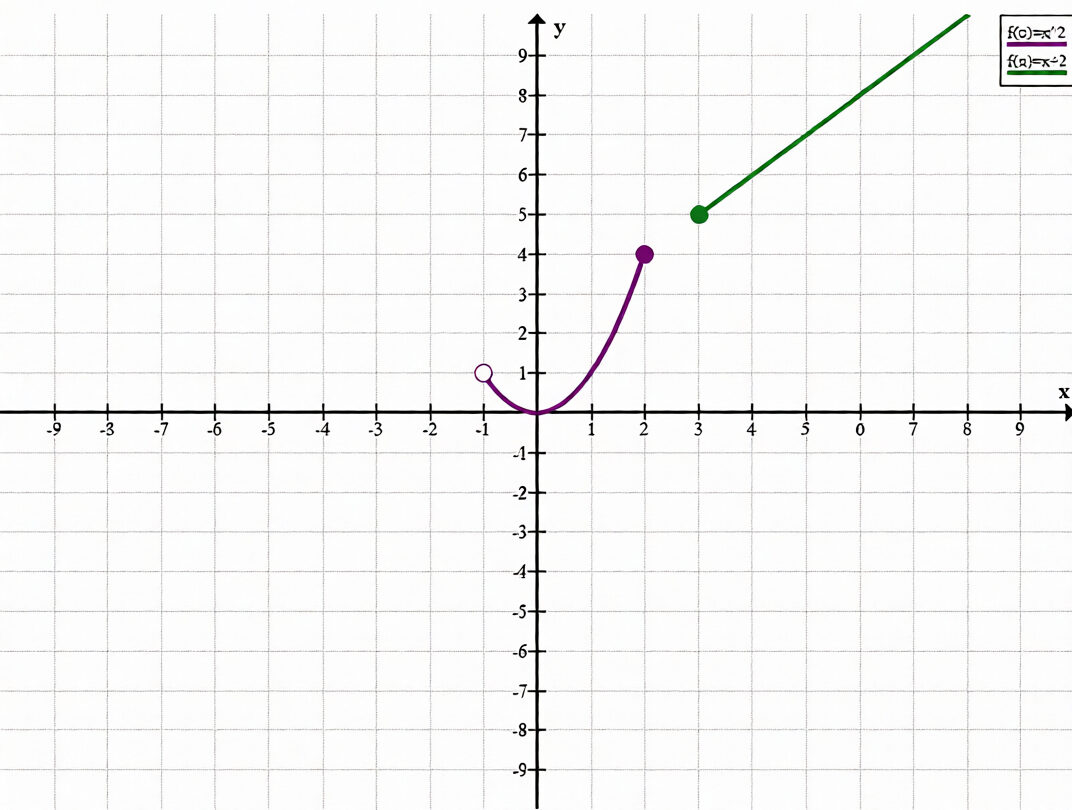
Пусть \(A\) — наибольшее значение функции \(y = x^2\) на полуинтервале \((-1; 2]\), а \(B\) — наименьшее значение функции \(y = -x + 2\) на луче \([3; +\infty)\). что больше: \(A\) или \(B\)? сделайте графическую иллюстрацию.
y = x², (−1; 2], Aнаиб = 4.
y = x + 2, [3; +∞), Bнаим = 3 + 2 = 5.
B > A.
Рассмотрим сначала функцию \(y = x^2\) на полуинтервале \([-3; 2)\).
этот промежуток включает левый конец \(x = -3\) и не включает правый конец \(x = 2\).
функция \(y = x^2\) убывает при \(x < 0\) и возрастает при \(x > 0\), достигая минимума в нуле.
значения на концах:
— при \(x = -3\): \(y = (-3)^2 = 9\);
— при \(x \to 2^{-}\): \(y \to 4\), но точка \(x = 2\) не входит, поэтому значение 4 не достигается, но близко к нему.
наибольшее значение достигается в \(x = -3\), так как \(|-3| > |x|\) для всех остальных \(x \in [-3; 2)\).
следовательно:
\[
A = 9
\]
теперь рассмотрим функцию \(y = 3x\) на луче \([-1; +\infty)\).
это линейная возрастающая функция (коэффициент \(3 > 0\)).
наименьшее значение достигается при наименьшем \(x\), то есть при \(x = -1\):
\[
B = 3 \cdot (-1) = -3
\]
сравниваем:
\[
A = 9, \quad B = -3 \Rightarrow A > B
\]
итоговые ответы:
\(A = 9\), \(B = -3\), следовательно, \(A > B\).