Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.50 Мордкович — Подробные Ответы
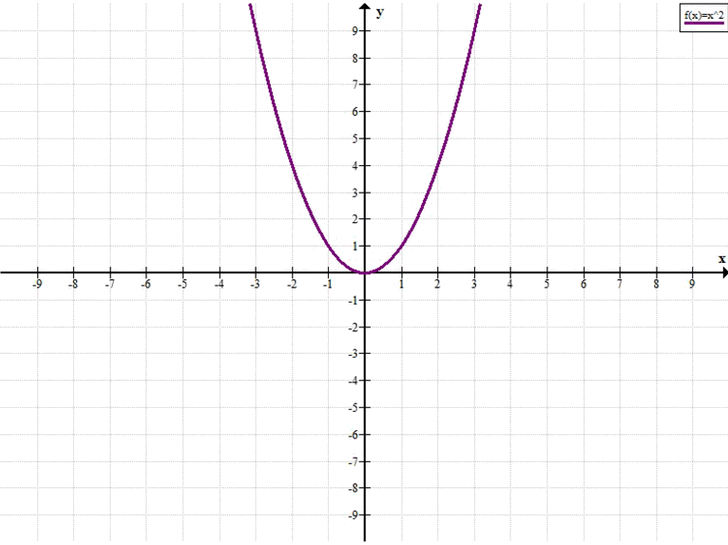
С помощью графика функции \(y = x^2\) определите, при каких значениях \(x\) выполняется неравенство:
а) \(x^2 < 1\);
б) \(x^2 \ge 1\);
в) \(x^2 \le 9\);
г) \(x^2 > 9\).
y = x²
a) x² < 1 ⇒ y < 1, x (-1; 1).
б) x² ≥ 1 ⇒ y ≥ 1, x (-∞; -1] и [1; +∞).
в) x² ≤ 9 ⇒ y ≤ 9, x [-3; 3].
г) x² > 9 ⇒ y > 9, x (-∞; -3) и (3; +∞).
Функция \(y = x^2\) — парабола, симметричная относительно оси ординат, с вершиной в точке \((0; 0)\).
Неравенства вида \(x^2 < a\) или \(x^2 > a\) решаются с учётом того, что \(x^2 = a\) при \(x = \pm\sqrt{a}\) (при \(a \ge 0\)).
а) Неравенство \(x^2 < 1\):
Решаем уравнение \(x^2 = 1\) → \(x = \pm1\).
Парабола ниже прямой \(y = 1\) между корнями.
Так как неравенство строгое, концы не включаются:
\[
x \in (-1; 1)
\]
б) Неравенство \(x^2 \ge 1\):
Значения \(x\), при которых график лежит на уровне \(y = 1\) или выше.
Это внешние части относительно корней \(x = \pm1\), включая их:
\[
x \in (-\infty; -1] \cup [1; +\infty)
\]
в) Неравенство \(x^2 \le 9\):
Решаем \(x^2 = 9\) → \(x = \pm3\).
График ниже или на уровне \(y = 9\) между корнями, включая их:
\[
x \in [-3; 3]
\]
г) Неравенство \(x^2 > 9\):
График выше уровня \(y = 9\) вне отрезка между корнями.
Концы не входят (строгое неравенство):
\[
x \in (-\infty; -3) \cup (3; +\infty)
\]
Итоговые ответы:
а) \(x \in (-1; 1)\)
б) \(x \in (-\infty; -1] \cup [1; +\infty)\)
в) \(x \in [-3; 3]\)
г) \(x \in (-\infty; -3) \cup (3; +\infty)\)