Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.51 Мордкович — Подробные Ответы
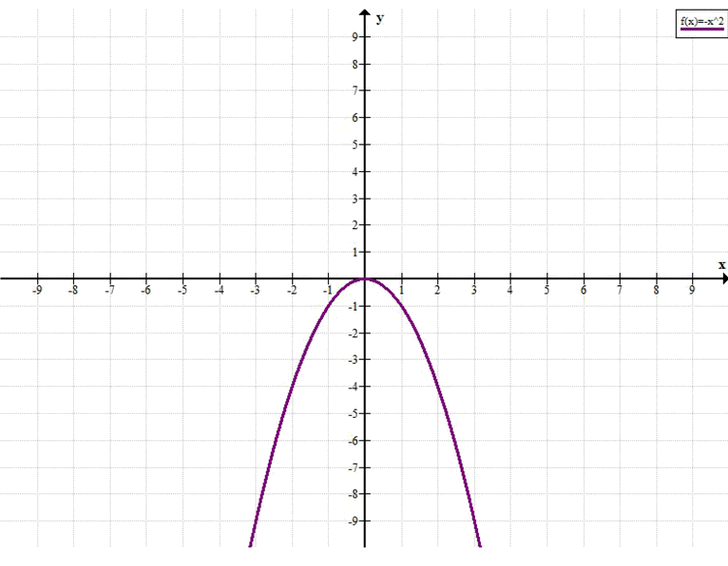
С помощью графика функции \(y = -x^2\) определите, при каких значениях \(x\) выполняется неравенство:
а) \(-x^2 > -4\);
б) \(-x^2 \le -4\);
в) \(-x^2 < -9\);
г) \(-x^2 \ge -9\).
y = -x²
a) -x² ≤ -4 ⇒ y ≤ -4, x (-∞; -2] и [2; +∞).
б) -x² > -9 ⇒ y > -9, x (-3; 3).
в) -x² ≥ -4 ⇒ y ≥ -4, x [-2; 2].
г) -x² < -9 ⇒ y < -9, x (-∞; -3) и (3; +∞).
Рассмотрим функцию \( y = -x^2 \). Это парабола, ветви которой направлены вниз, с вершиной в точке \( (0; 0) \). Она чётная: \( y(-x) = y(x) \). Значения функции всегда неположительны: \( y \leq 0 \) для любого \( x \in \mathbb{R} \).
Требуется проанализировать четыре неравенства, связанных с этой функцией, и обосновать указанные множества решений.
\[
y = -x^2
\]
Часть a) Неравенство \( -x^2 \leq -4 \)
Преобразуем неравенство:
\[
-x^2 \leq -4
\]
Умножим обе части на \( -1 \). При умножении на отрицательное число знак неравенства меняется:
\[
x^2 \geq 4
\]
Это эквивалентно:
\[
|x| \geq 2
\]
Что означает:
\[
x \leq -2 \quad \text{или} \quad x \geq 2
\]
\[
x \in (-\infty; -2] \cup [2; +\infty)
\]
Для всех таких \( x \) значение функции \( y = -x^2 \leq -4 \), так как при \( x = \pm 2 \) получаем \( y = -4 \), а при \( |x| > 2 \) — \( y < -4 \).
Следовательно, утверждение верно.
Часть б) Неравенство \( -x^2 > -9 \)
Преобразуем:
\[
-x^2 > -9
\]
Умножим обе части на \( -1 \) (знак неравенства меняется):
\[
x^2 < 9
\]
Это эквивалентно:
\[
|x| < 3
\]
Что означает:
\[
-3 < x < 3
\]
\[
x \in (-3; 3)
\]
Для любого \( x \) из этого интервала: \( x^2 < 9 \Rightarrow -x^2 > -9 \Rightarrow y > -9 \).
Границы \( x = \pm 3 \) не входят, так как при них \( y = -9 \), а требуется строгое неравенство.
Утверждение верно.
Часть в) Неравенство \( -x^2 \geq -4 \)
Преобразуем:
\[
-x^2 \geq -4
\]
Умножим на \( -1 \) (знак меняется):
\[
x^2 \leq 4
\]
Это эквивалентно:
\[
|x| \leq 2
\]
Что означает:
\[
-2 \leq x \leq 2
\]
\[
x \in [-2; 2]
\]
При \( x = \pm 2 \): \( y = -4 \), что удовлетворяет условию \( \geq -4 \).
При \( |x| < 2 \): \( y > -4 \), что также подходит.
Следовательно, утверждение верно.
Часть г) Неравенство \( -x^2 < -9 \)
Преобразуем:
\[
-x^2 < -9
\]
Умножим на \( -1 \) (знак меняется):
\[
x^2 > 9
\]
Это эквивалентно:
\[
|x| > 3
\]
Что означает:
\[
x < -3 \quad \text{или} \quad x > 3
\]
\[
x \in (-\infty; -3) \cup (3; +\infty)
\]
При таких \( x \): \( x^2 > 9 \Rightarrow -x^2 < -9 \Rightarrow y < -9 \).
Границы \( x = \pm 3 \) не входят, так как при них \( y = -9 \), а требуется строгое неравенство.
Утверждение верно.
Все четыре утверждения корректны и полностью соответствуют свойствам функции \( y = -x^2 \), которая является чётной, убывающей на \( [0; +\infty) \) и возрастающей на \( (-\infty; 0] \), с максимумом в нуле.
Ответы:
a) -x² ≤ -4 ⇒ y ≤ -4, x (-∞; -2] и [2; +∞).
б) -x² > -9 ⇒ y > -9, x (-3; 3).
в) -x² ≥ -4 ⇒ y ≥ -4, x [-2; 2].
г) -x² < -9 ⇒ y < -9, x (-∞; -3) и (3; +∞).