Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 44.52 Мордкович — Подробные Ответы
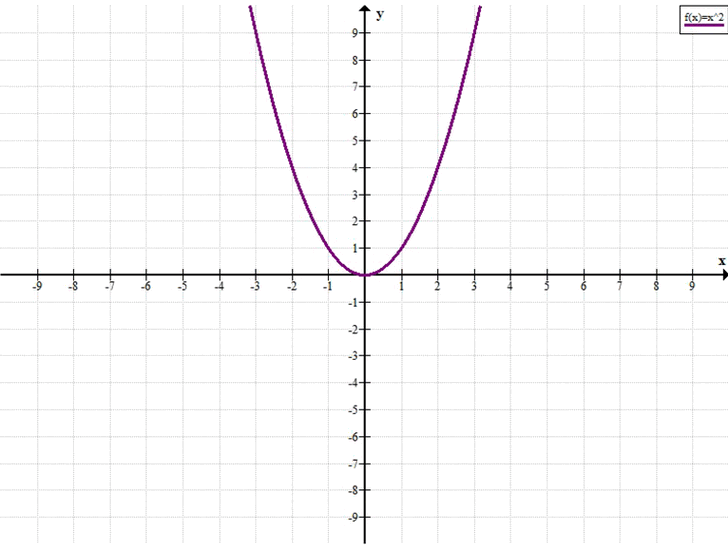
Используя график функции \( y = x^2 \), определите, при каких значениях \( x \) выполняется неравенство:
а) \( 1 < x^2 < 4 \)
б) \( 4 \leqslant x^2 \leqslant 9 \)
y = x²
a) 1 < x² < 4 ⇒ 1 < y < 4, x (-2; -1) и (1; 2).
б) 4 ≤ x² ≤ 9 ⇒ 4 ≤ y ≤ 9, x [-3; -2] и [2; 3].
Рассмотрим функцию \( y = x^2 \). Это чётная парабола, ветви направлены вверх, вершина в точке \( (0; 0) \). Функция убывает на \( (-\infty; 0] \) и возрастает на \( [0; +\infty) \). Для решения двойных неравенств вида \( a < x^2 < b \) или \( a \leq x^2 \leq b \) (где \( 0 \leq a < b \)) удобно использовать свойство модуля: \( x^2 < c \iff |x| < \sqrt{c} \), а \( x^2 > c \iff |x| > \sqrt{c} \).
\[
y = x^2
\]
Часть a) Неравенство \( 1 < x^2 < 4 \)
Разобьём двойное неравенство на два:
\[
x^2 > 1 \quad \text{и} \quad x^2 < 4
\]
Решим первое:
\[
x^2 > 1 \Rightarrow |x| > 1 \Rightarrow x < -1 \quad \text{или} \quad x > 1
\]
\[
x \in (-\infty; -1) \cup (1; +\infty)
\]
Решим второе:
\[
x^2 < 4 \Rightarrow |x| < 2 \Rightarrow -2 < x < 2
\]
\[
x \in (-2; 2)
\]
Найдём пересечение этих множеств:
\[
\big( (-\infty; -1) \cup (1; +\infty) \big) \cap (-2; 2) = (-2; -1) \cup (1; 2)
\]
Для любого \( x \) из этого множества:
\[
1 < x^2 < 4 \Rightarrow 1 < y < 4
\]
Границы \( x = \pm 1 \) и \( x = \pm 2 \) не входят, так как неравенства строгие.
Следовательно, утверждение верно.
Часть б) Неравенство \( 4 \leq x^2 \leq 9 \)
Разобьём на два:
\[
x^2 \geq 4 \quad \text{и} \quad x^2 \leq 9
\]
Решим первое:
\[
x^2 \geq 4 \Rightarrow |x| \geq 2 \Rightarrow x \leq -2 \quad \text{или} \quad x \geq 2
\]
\[
x \in (-\infty; -2] \cup [2; +\infty)
\]
Решим второе:
\[
x^2 \leq 9 \Rightarrow |x| \leq 3 \Rightarrow -3 \leq x \leq 3
\]
\[
x \in [-3; 3]
\]
Найдём пересечение:
\[
\big( (-\infty; -2] \cup [2; +\infty) \big) \cap [-3; 3] = [-3; -2] \cup [2; 3]
\]
Для любого \( x \) из этого множества:
\[
4 \leq x^2 \leq 9 \Rightarrow 4 \leq y \leq 9
\]
Границы \( x = \pm 2 \) и \( x = \pm 3 \) входят, так как неравенства нестрогие.
Следовательно, утверждение верно.
\[
\text{a) } x \in (-2; -1) \cup (1; 2)
\]
\[
\text{б) } x \in [-3; -2] \cup [2; 3]
\]