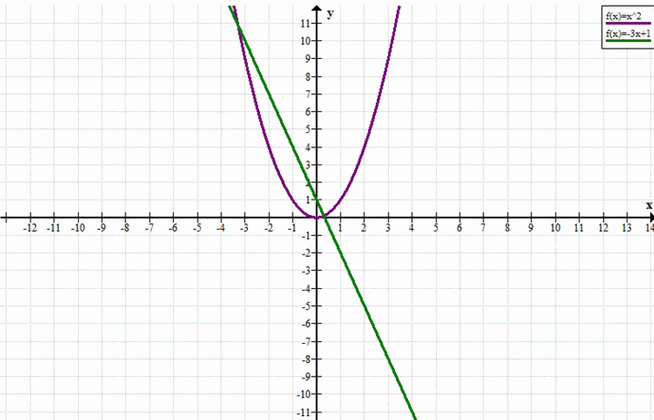ГДЗ по Алгебре 7 Класс Номер 45.12 Мордкович — Подробные Ответы

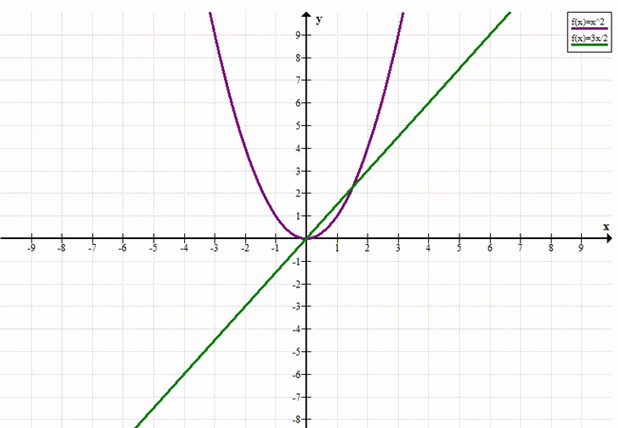
Определите, сколько корней имеет уравнение: а) \(x^2\) = \(\frac{3x}{2}\); б) \(х^2\) = -х — 3; в) \(x^2\) = \(-\frac{x+1}{4}\); г) \(x^2\) = -3х + 1.

а)
\( x^2 = \frac{3x}{2} \)
\( 2x^2 = 3x \)
\( 2x^2 — 3x = 0 \)
\( x(2x — 3) = 0 \)
\( x_1 = 0 \)
\( 2x — 3 = 0 \)
\( 2x = 3 \)
\( x_2 = \frac{3}{2} \)

Ответ: 2 корня

б)
\( x^2 = -x — 3 \)
\( x^2 + x + 3 = 0 \)
\( D = b^2 — 4ac \)
\( D = 1^2 — 4 \cdot 1 \cdot 3 \)
\( D = 1 — 12 \)
\( D = -11 \)

Ответ: 0 корней

в)
\( x^2 = -\frac{x+1}{4} \)
\( 4x^2 = -(x+1) \)
\( 4x^2 = -x — 1 \)
\( 4x^2 + x + 1 = 0 \)
\( D = b^2 — 4ac \)
\( D = 1^2 — 4 \cdot 4 \cdot 1 \)
\( D = 1 — 16 \)
\( D = -15 \)

Ответ: 0 корней

г)
\( x^2 = -3x + 1 \)
\( x^2 + 3x — 1 = 0 \)
\( D = b^2 — 4ac \)
\( D = 3^2 — 4 \cdot 1 \cdot (-1) \)
\( D = 9 + 4 \)
\( D = 13 \)

Ответ: 2 корня

а) \(x^2 = \frac{3x}{2}\)

Умножим обе части уравнения на 2, чтобы избавиться от знаменателя (это допустимо, так как 2 ≠ 0):
\[
2x^2 = 3x.
\]

Перенесём все члены в левую часть:
\[
2x^2 — 3x = 0.
\]

Вынесем общий множитель \(x\) за скобки:
\[
x(2x — 3) = 0.
\]

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Поэтому решаем два простых уравнения:

1. \(x = 0\),
2. \(2x — 3 = 0 \Rightarrow 2x = 3 \Rightarrow x = \frac{3}{2}\).

Оба значения удовлетворяют исходному уравнению. Проверим кратко:

— При \(x = 0\): \(0^2 = 0\), \(\frac{3 \cdot 0}{2} = 0\) → верно.
— При \(x = \frac{3}{2}\): \(\left(\frac{3}{2}\right)^2 = \frac{9}{4}\), \(\frac{3 \cdot \frac{3}{2}}{2} = \frac{9}{4}\) → верно.

Графически это означает, что парабола \(y = x^2\) и прямая \(y = \frac{3}{2}x\) пересекаются в двух точках: \((0; 0)\) и \(\left(\frac{3}{2}; \frac{9}{4}\right)\).

Ответ: 2 корня.

б) \(x^2 = -x — 3\)

Перенесём все члены в левую часть, чтобы получить стандартный вид квадратного уравнения:
\[
x^2 + x + 3 = 0.
\]

Здесь коэффициенты: \(a = 1\), \(b = 1\), \(c = 3\).

Вычислим дискриминант по формуле \(D = b^2 — 4ac\):
\[
D = 1^2 — 4 \cdot 1 \cdot 3 = 1 — 12 = -11.
\]

Поскольку \(D < 0\), уравнение **не имеет действительных корней**. Это означает, что не существует такого действительного числа \(x\), при котором левая и правая части уравнения были бы равны.

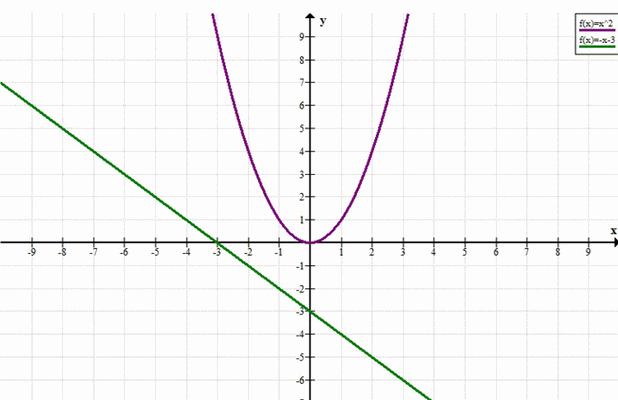
Геометрически: график функции \(y = x^2\) (парабола, ветви вверх) и график функции \(y = -x — 3\) (прямая с отрицательным наклоном) не пересекаются. Парабола всегда «выше» прямой, поэтому решений нет.

Ответ: 0 корней.

в) \(x^2 = -\frac{x + 1}{4}\)

Умножим обе части уравнения на 4, чтобы избавиться от дроби:
\[
4x^2 = -(x + 1).
\]

Раскроем скобки в правой части:
\[
4x^2 = -x — 1.
\]

Перенесём все члены в левую часть:
\[
4x^2 + x + 1 = 0.
\]

Это квадратное уравнение с коэффициентами: \(a = 4\), \(b = 1\), \(c = 1\).

Найдём дискриминант:
\[
D = b^2 — 4ac = 1^2 — 4 \cdot 4 \cdot 1 = 1 — 16 = -15.
\]

Так как \(D = -15 < 0\), уравнение не имеет действительных решений.

Можно также заметить, что левая часть \(x^2\) всегда неотрицательна (\(x^2 \geq 0\)), а правая часть \(-\frac{x + 1}{4}\) может быть положительной только при \(x < -1\). Однако даже в этой области значения не совпадают, что подтверждается отрицательным дискриминантом.

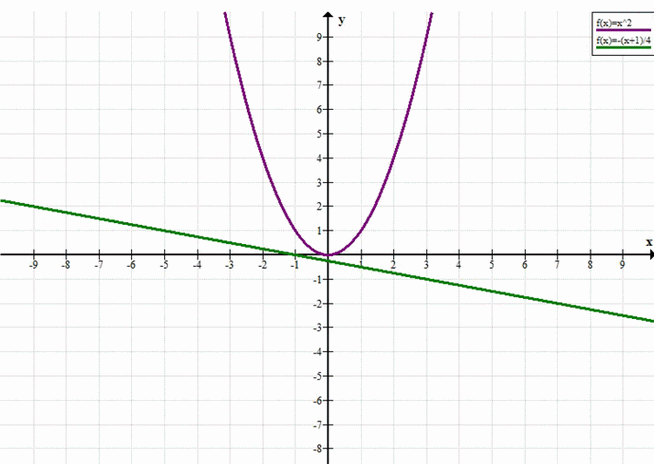
График \(y = x^2\) и график \(y = -\frac{x + 1}{4}\) не имеют общих точек.

Ответ: 0 корней.

г) \(x^2 = -3x + 1\)

Перенесём все члены в левую часть:
\[
x^2 + 3x — 1 = 0.
\]

Коэффициенты: \(a = 1\), \(b = 3\), \(c = -1\).

Вычислим дискриминант:
\[
D = b^2 — 4ac = 3^2 — 4 \cdot 1 \cdot (-1) = 9 + 4 = 13.
\]

Поскольку \(D = 13 > 0\), уравнение имеет два различных действительных корня. Хотя в задании не требуется находить сами корни, отметим, что они равны:
\[
x = \frac{-3 \pm \sqrt{13}}{2}.
\]

Оба корня — иррациональные числа, но они существуют в множестве действительных чисел.

Геометрически: парабола \(y = x^2\) и прямая \(y = -3x + 1\) пересекаются в двух точках, так как прямая «пересекает» параболу слева и справа от её вершины.

Ответ: 2 корня.