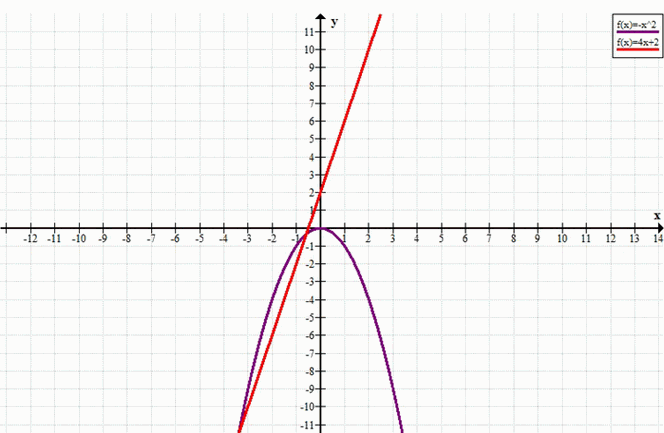ГДЗ по Алгебре 7 Класс Номер 45.13 Мордкович — Подробные Ответы

а) \(-x^2 = 4 — x;\)

б) \(\frac{2x — 1}{2} = -x^2;\)

в) \(-x^2 = \frac{4}{3}x;\)

г) \(4x + 2 = -x^2.\)

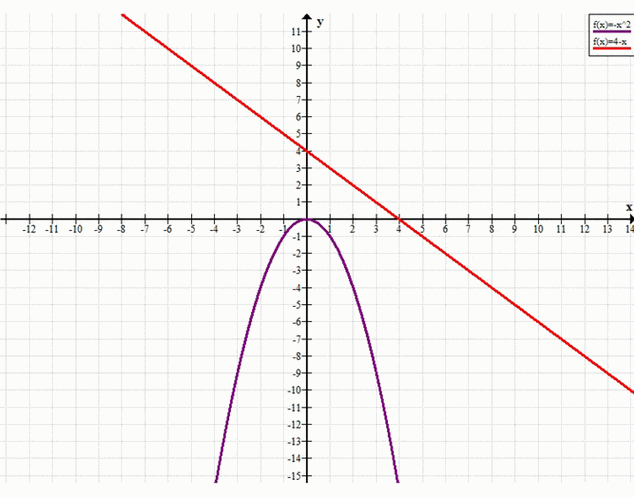
а) –x² = 4 – x
y = –x², y = 4 – x

Ответ: нет решений.

б) (2x – 1):2 = –x²
y = (2x – 1):2, y = –x²

Ответ: два решения.

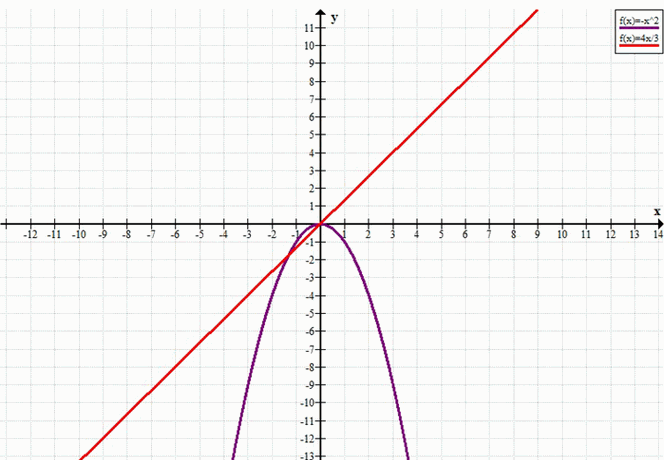
в) –x² = 4:3 x
y = –x², y = 4:3 x

Ответ: два решения.

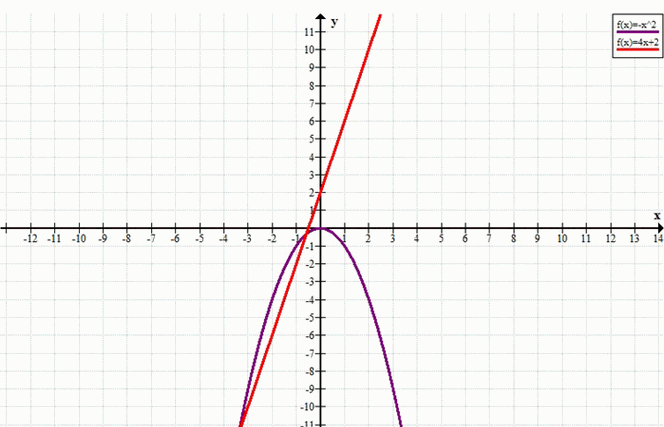
г) 4x + 2 = –x²
y = 4x + 2, y = –x²

Ответ: два решения.

а) \(-x^2 = 4 — x\)

Перепишем уравнение в стандартном виде, перенеся все члены в одну сторону:
\[
-x^2 + x — 4 = 0.
\]

Умножим обе части на \(-1\) для удобства:
\[
x^2 — x + 4 = 0.
\]

Это квадратное уравнение с коэффициентами:
\(a = 1\), \(b = -1\), \(c = 4\).

Найдём дискриминант:
\[
D = b^2 — 4ac = (-1)^2 — 4 \cdot 1 \cdot 4 = 1 — 16 = -15.
\]

Поскольку \(D < 0\), уравнение не имеет действительных корней. Это означает, что графики функций \(y = -x^2\) (парабола, ветви вниз) и \(y = 4 — x\) (прямая с отрицательным наклоном) не пересекаются. Следовательно, решений в области действительных чисел нет.

Ответ: нет решений.

б) \(\frac{2x — 1}{2} = -x^2\)

Приведём уравнение к стандартному виду. Умножим обе части на 2, чтобы избавиться от знаменателя:
\[
2x — 1 = -2x^2.
\]

Перенесём все члены в левую часть:
\[
2x^2 + 2x — 1 = 0.
\]

Коэффициенты: \(a = 2\), \(b = 2\), \(c = -1\).

Вычислим дискриминант:
\[
D = b^2 — 4ac = 2^2 — 4 \cdot 2 \cdot (-1) = 4 + 8 = 12.
\]

Так как \(D = 12 > 0\), уравнение имеет **два различных действительных корня**. Графически это означает, что прямая \(y = \frac{2x — 1}{2}\) и парабола \(y = -x^2\) пересекаются в двух точках.

Ответ: два решения.

в) \(-x^2 = \frac{4}{3}x\)

Перенесём все члены в одну сторону:
\[
-x^2 — \frac{4}{3}x = 0.
\]

Умножим обе части на 3, чтобы избавиться от дроби:
\[
-3x^2 — 4x = 0.
\]

Можно вынести общий множитель \(-x\):
\[
-x(3x + 4) = 0.
\]

Произведение равно нулю, когда хотя бы один из множителей равен нулю:
\[
-x = 0 \quad \Rightarrow \quad x = 0,
\]

\[
3x + 4 = 0 \quad \Rightarrow \quad x = -\frac{4}{3}.
\]

Таким образом, уравнение имеет два действительных корня: \(x = 0\) и \(x = -\frac{4}{3}\). Это подтверждает, что графики \(y = -x^2\) и \(y = \frac{4}{3}x\) пересекаются в двух точках.

Ответ: два решения.

г) \(4x + 2 = -x^2\)

Перенесём все члены в левую часть:
\[
x^2 + 4x + 2 = 0.
\]

Коэффициенты: \(a = 1\), \(b = 4\), \(c = 2\).

Найдём дискриминант:
\[
D = b^2 — 4ac = 4^2 — 4 \cdot 1 \cdot 2 = 16 — 8 = 8.
\]

Поскольку \(D = 8 > 0\), уравнение имеет два различных действительных корня. Графики функций \(y = 4x + 2\) (прямая) и \(y = -x^2\) (парабола, ветви вниз) пересекаются в двух точках.

Ответ: два решения.