ГДЗ по Алгебре 7 Класс Номер 45.15 Мордкович — Подробные Ответы

а) \(\frac{x^3 — x^2}{x — 1} = -2x + 3;\)

б) \(-\frac{x^3 + 2x^2}{x + 2} = x — 2;\)

в) \(\frac{x^3 — 3x^2}{x — 3} = x + 6;\)

г) \(-\frac{4x^2 + x^3}{x + 4} = 2x — 8.\)

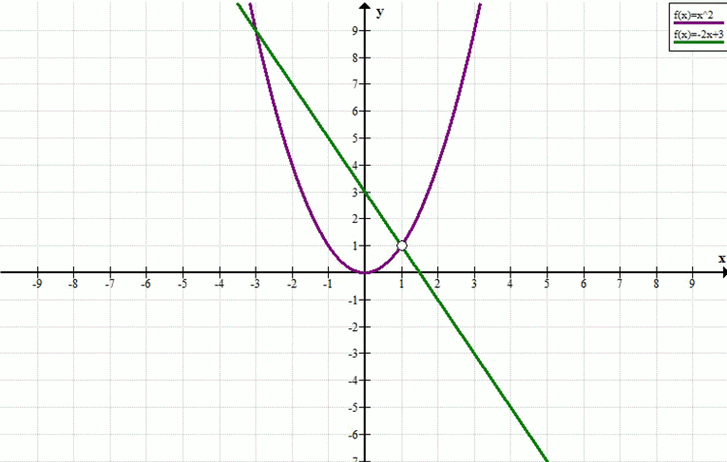
а) \(\frac{x^3 — x^2}{x — 1} = -2x + 3\)

\(y = \frac{x^3 — x^2}{x — 1} = \frac{x^2(x — 1)}{x — 1} = x^2,\quad x \ne 1,\quad y = -2x + 3\)

Ответ: \(x = -3\).

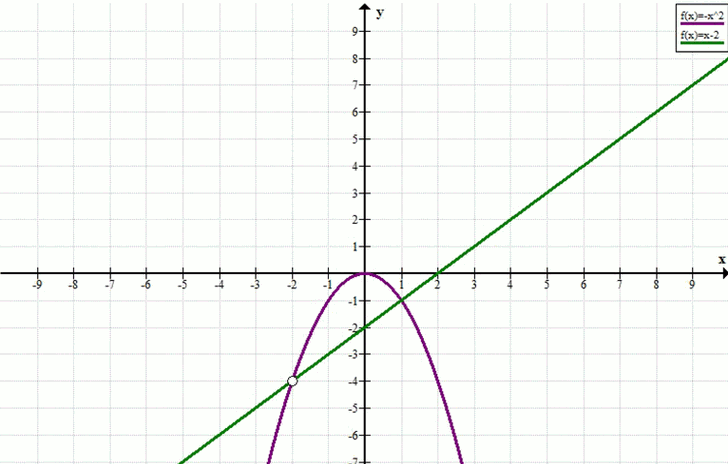
б) \(-\frac{x^3 + 2x^2}{x + 2} = x — 2\)

\(y = -\frac{x^3 + 2x^2}{x + 2} = -\frac{x^2(x + 2)}{x + 2} = -x^2,\quad x \ne -2,\quad y = x — 2\)

Ответ: \(x = 1\).

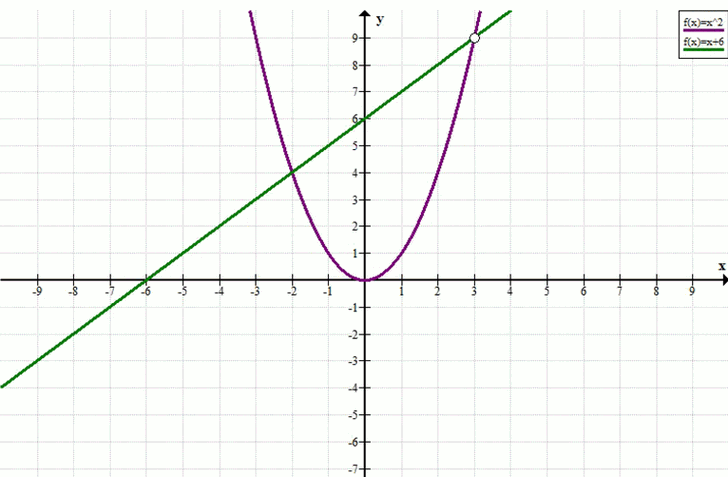
в) \(\frac{x^3 — 3x^2}{x — 3} = x + 6\)

\(y = \frac{x^3 — 3x^2}{x — 3} = \frac{x^2(x — 3)}{x — 3} = x^2,\quad x \ne 3,\quad y = x + 6\)

Ответ: \(x = -2\).

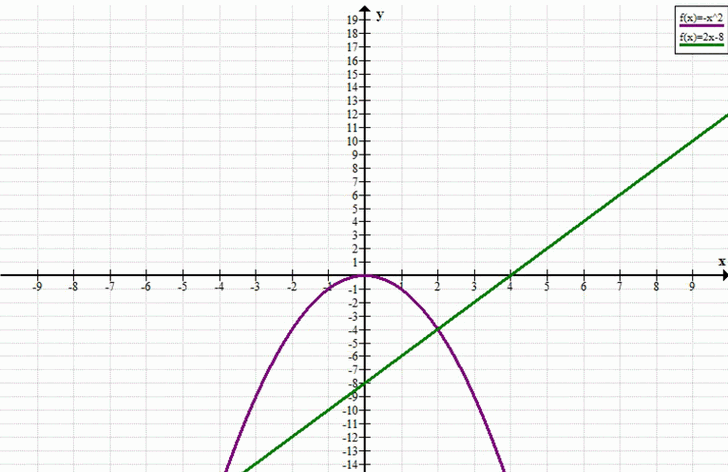
г) \(-\frac{4x^2 + x^3}{x + 4} = 2x — 8\)

\(y = -\frac{4x^2 + x^3}{x + 4} = -\frac{x^2(4 + x)}{x + 4} = -x^2,\quad x \ne -4,\quad y = 2x — 8\)

Ответ: \(x = 2\).

а) \(\frac{x^3 — x^2}{x — 1} = -2x + 3\)

Сначала упростим левую часть. Вынесем общий множитель в числителе:
\[
x^3 — x^2 = x^2(x — 1).
\]

Тогда при \(x \ne 1\) (чтобы знаменатель не обращался в ноль) дробь сокращается:
\[
\frac{x^2(x — 1)}{x — 1} = x^2.
\]

Уравнение принимает вид:
\[
x^2 = -2x + 3.
\]

Переносим все члены в левую часть:
\[
x^2 + 2x — 3 = 0.
\]

Решаем квадратное уравнение. Дискриминант:
\[
D = 2^2 — 4 \cdot 1 \cdot (-3) = 4 + 12 = 16.
\]

Корни:
\[
x = \frac{-2 \pm \sqrt{16}}{2} = \frac{-2 \pm 4}{2} \Rightarrow x_1 = 1,\quad x_2 = -3.
\]

Проверяем ОДЗ: \(x \ne 1\), поэтому \(x = 1\) отбрасываем. Остаётся:
\[
x = -3.
\]

Проверка в исходном уравнении:
— Левая часть: \(\frac{(-3)^3 — (-3)^2}{-3 — 1} = \frac{-27 — 9}{-4} = \frac{-36}{-4} = 9\),
— Правая часть: \(-2(-3) + 3 = 6 + 3 = 9\).

Верно.

Графически: функция \(y = x^2\) (с выколотой точкой при \(x = 1\)) и прямая \(y = -2x + 3\) пересекаются в точке \(x = -3\).

Ответ: \(x = -3\).

б) \(-\frac{x^3 + 2x^2}{x + 2} = x — 2\)

Вынесем общий множитель в числителе:
\[
x^3 + 2x^2 = x^2(x + 2).
\]

При \(x \ne -2\) дробь упрощается:
\[
-\frac{x^2(x + 2)}{x + 2} = -x^2.
\]

Уравнение становится:
\[
-x^2 = x — 2.
\]

Переносим всё в левую часть:
\[
-x^2 — x + 2 = 0 \quad \text{или} \quad x^2 + x — 2 = 0.
\]

Дискриминант:
\[
D = 1^2 — 4 \cdot 1 \cdot (-2) = 1 + 8 = 9.
\]

Корни:
\[
x = \frac{-1 \pm 3}{2} \Rightarrow x_1 = 1,\quad x_2 = -2.
\]

Но \(x = -2\) недопустимо (знаменатель равен нулю), поэтому:
\[
x = 1.
\]

Проверка:
— Левая часть: \(-\frac{1^3 + 2 \cdot 1^2}{1 + 2} = -\frac{1 + 2}{3} = -1\),
— Правая часть: \(1 — 2 = -1\).

Верно.

График функции \(y = -x^2\) (с выколотой точкой при \(x = -2\)) пересекает прямую \(y = x — 2\) в точке \(x = 1\).

Ответ: \(x = 1\).

в) \(\frac{x^3 — 3x^2}{x — 3} = x + 6\)

Числитель: \(x^3 — 3x^2 = x^2(x — 3)\).
При \(x \ne 3\) сокращаем:
\[
\frac{x^2(x — 3)}{x — 3} = x^2.
\]

Получаем уравнение:
\[
x^2 = x + 6 \quad \Rightarrow \quad x^2 — x — 6 = 0.
\]

Дискриминант:
\[
D = (-1)^2 — 4 \cdot 1 \cdot (-6) = 1 + 24 = 25.
\]

Корни:
\[
x = \frac{1 \pm 5}{2} \Rightarrow x_1 = 3,\quad x_2 = -2.
\]

Но \(x = 3\) исключено из ОДЗ (\(x \ne 3\)), остаётся:
\[
x = -2.
\]

Проверка:
— Левая часть: \(\frac{(-2)^3 — 3(-2)^2}{-2 — 3} = \frac{-8 — 12}{-5} = \frac{-20}{-5} = 4\),
— Правая часть: \(-2 + 6 = 4\).

Верно.

Графически: парабола \(y = x^2\) (без точки \(x = 3\)) и прямая \(y = x + 6\) пересекаются в точке \(x = -2\).

Ответ: \(x = -2\).

г) \(-\frac{4x^2 + x^3}{x + 4} = 2x — 8\)

Перепишем числитель в стандартном порядке:
\[
x^3 + 4x^2 = x^2(x + 4).
\]

Тогда при \(x \ne -4\):
\[
-\frac{x^2(x + 4)}{x + 4} = -x^2.
\]

Уравнение:
\[
-x^2 = 2x — 8 \quad \Rightarrow \quad x^2 + 2x — 8 = 0.
\]

Дискриминант:
\[
D = 2^2 — 4 \cdot 1 \cdot (-8) = 4 + 32 = 36.
\]

Корни:
\[
x = \frac{-2 \pm 6}{2} \Rightarrow x_1 = 2,\quad x_2 = -4.
\]

Но \(x = -4\) запрещено (знаменатель ноль), поэтому:
\[
x = 2.
\]

Проверка:
— Левая часть: \(-\frac{4 \cdot 2^2 + 2^3}{2 + 4} = -\frac{16 + 8}{6} = -\frac{24}{6} = -4\),
— Правая часть: \(2 \cdot 2 — 8 = 4 — 8 = -4\).

Верно.

График функции \(y = -x^2\) (с выколотой точкой при \(x = -4\)) пересекает прямую \(y = 2x — 8\) в точке \(x = 2\).

Ответ: \(x = 2\).