Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 45.2 Мордкович — Подробные Ответы
Решите графически уравнение: а) х² = 1; б)х²=4; в)х²=0; г)х²=-1.
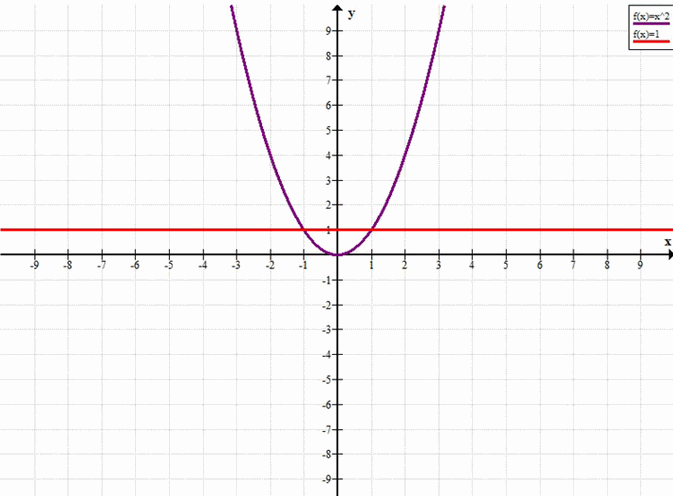
а)
\( x^2 = 1 \)
\( y = x^2 \)
\( y = 1 \)
Графики функций \( y = x^2 \) и \( y = 1 \) пересекаются в точках с абсциссами \( x = -1 \) и \( x = 1 \).
Ответ: -1, 1
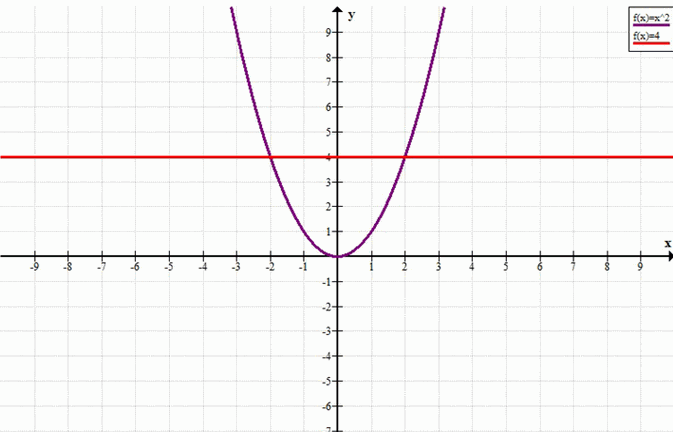
б)
\( x^2 = 4 \)
\( y = x^2 \)
\( y = 4 \)
Графики функций \( y = x^2 \) и \( y = 4 \) пересекаются в точках с абсциссами \( x = -2 \) и \( x = 2 \).
Ответ: -2, 2
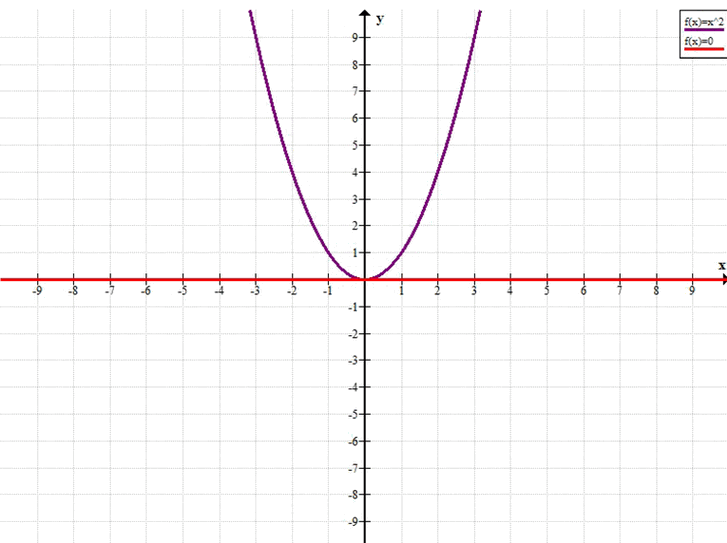
в)
\( x^2 = 0 \)
\( y = x^2 \)
\( y = 0 \)
Графики функций \( y = x^2 \) и \( y = 0 \) пересекаются в точке с абсциссой \( x = 0 \).
Ответ: 0
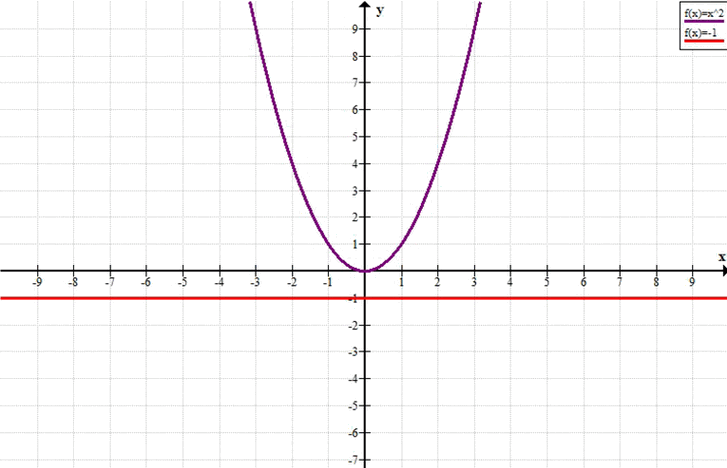
г)
\( x^2 = -1 \)
\( y = x^2 \)
\( y = -1 \)
График функции \( y = x^2 \) (парабола, ветви которой направлены вверх и вершина находится в начале координат) не пересекается с графиком функции \( y = -1 \) (горизонтальная прямая ниже оси абсцисс).
Ответ: нет решений
Условие: Решить графически уравнения:
а)
\(x^2 = 1\);
б)
\(x^2 = 4\);
в)
\(x^2 = 0\);
г)
\(x^2 = -1\).
Решение:
Для решения этих уравнений графически, мы построим график функции \(y = x^2\) и графики горизонтальных линий \(y = 1\), \(y = 4\), \(y = 0\) и \(y = -1\). Точки пересечения этих графиков будут являться решениями соответствующих уравнений.
а)
\(x^2 = 1\)
Построим график функции \(y = x^2\) (парабол
а) и график линии \(y = 1\).
График \(y = x^2\) проходит через точки \((-2, 4), (-1, 1), (0, 0), (1, 1), (2, 4)\).
Линия \(y = 1\) является горизонтальной линией, проходящей через точку \((0, 1)\).
Пересечение графиков происходит в точках, где \(x^2 = 1\). Это происходит при \(x = 1\) и \(x = -1\).
б)
\(x^2 = 4\)
Построим график функции \(y = x^2\) и график линии \(y = 4\).
Линия \(y = 4\) является горизонтальной линией, проходящей через точку \((0, 4)\).
Пересечение графиков происходит в точках, где \(x^2 = 4\). Это происходит при \(x = 2\) и \(x = -2\).
в)
\(x^2 = 0\)
Построим график функции \(y = x^2\) и график линии \(y = 0\).
Линия \(y = 0\) совпадает с осью абсцисс (осью x).
Пересечение графиков происходит в точке, где \(x^2 = 0\). Это происходит при \(x = 0\).
г)
\(x^2 = -1\)
Построим график функции \(y = x^2\) и график линии \(y = -1\).
Линия \(y = -1\) является горизонтальной линией, проходящей через точку \((0, -1)\).
График функции \(y = x^2\) всегда находится выше или на оси x (то есть \(y \ge 0\)).
Линия \(y = -1\) находится ниже оси x.
Следовательно, графики не пересекаются. Уравнение \(x^2 = -1\) не имеет действительных решений.
Ответы:
а)\(x = 1, x = -1\)
б)\(x = 2, x = -2\)
в)\(x = 0\)
г) Нет решений