ГДЗ по Алгебре 7 Класс Номер 45.9 Мордкович — Подробные Ответы

Решите графически уравнение: а) х² + 2х — 3 = 0; б) х²- 4\(x = -3\); в) х² + 4x + 3 = 0; г) х² — \(x = 6.\)

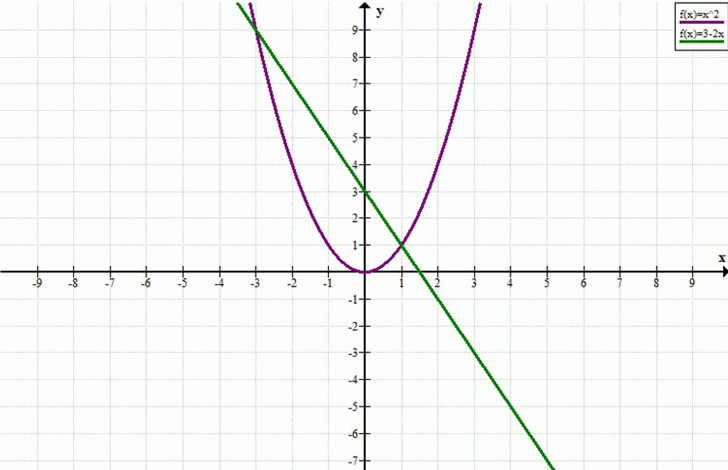
а) x² + 2x – 3 = 0
x² = 3 – 2x
y = x², y = 3 – 2x

Ответ: x = –3, x = 1.

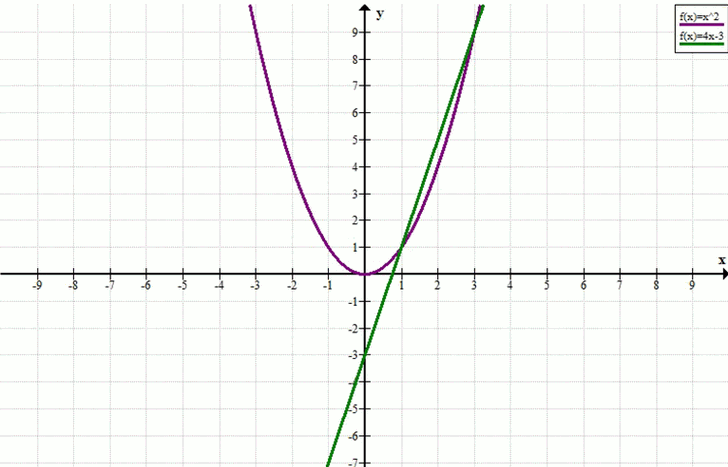
б) x² – 4x = –3
x² = 4x – 3
y = x², y = 4x – 3

Ответ: x = 1, x = 3.

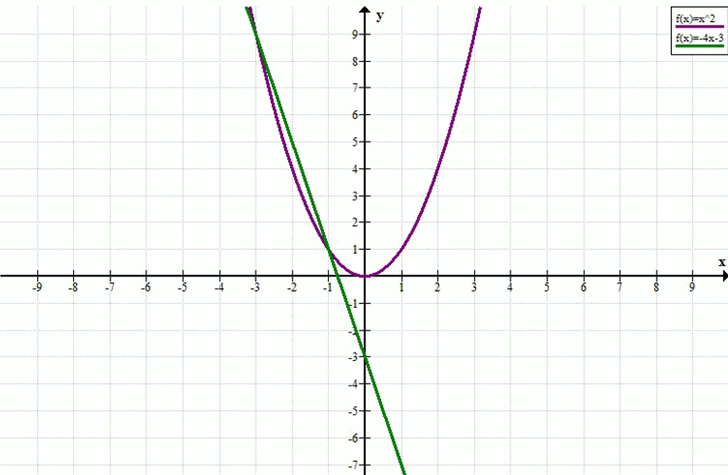
в) x² + 4x + 3 = 0
x² = –4x – 3
y = x², y = –4x – 3

Ответ: x = –3, x = –1.

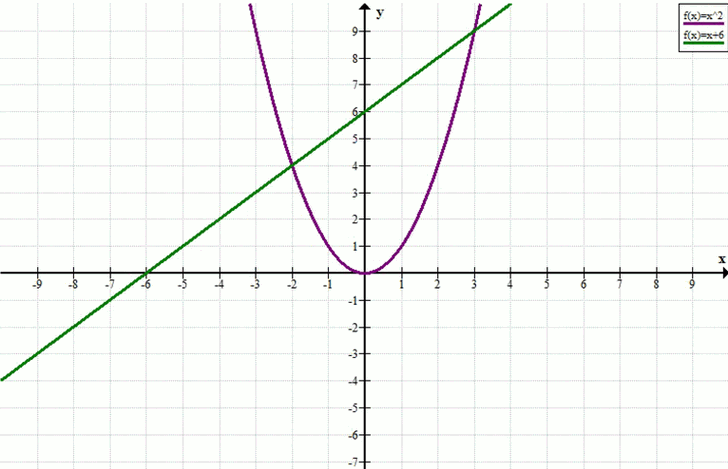
г) x² – x = 6
x² = x + 6
y = x², y = x + 6

Ответ: x = –2, x = 3.

а) \(x^2 + 2x — 3 = 0\)

Перенесём все члены, кроме \(x^2\), в правую часть:
\[
x^2 = 3 — 2x.
\]

Это уравнение можно интерпретировать как равенство двух функций:
\[
y = x^2 \quad \text{и} \quad y = 3 — 2x.
\]

Точки пересечения этих графиков (параболы и прямой) дают решения исходного уравнения. Чтобы найти их аналитически, подставим одно выражение в другое — но так как мы уже выразили \(x^2\), достаточно решить квадратное уравнение напрямую:

\[
x^2 + 2x — 3 = 0.
\]

Найдём дискриминант:
\[
D = 2^2 — 4 \cdot 1 \cdot (-3) = 4 + 12 = 16.
\]

Корни:
\[
x = \frac{-2 \pm \sqrt{16}}{2} = \frac{-2 \pm 4}{2}.
\]

Получаем:
— \(x_1 = \frac{-2 + 4}{2} = \frac{2}{2} = 1\),
— \(x_2 = \frac{-2 — 4}{2} = \frac{-6}{2} = -3\).

Проверка:
— При \(x = 1\): \(1^2 + 2 \cdot 1 — 3 = 1 + 2 — 3 = 0\) — верно.
— При \(x = -3\): \((-3)^2 + 2 \cdot (-3) — 3 = 9 — 6 — 3 = 0\) — верно.

Ответ: \(x = -3,\ x = 1\).

б) \(x^2 — 4x = -3\)

Перенесём \(-3\) в левую часть или выразим \(x^2\):
\[
x^2 = 4x — 3.
\]

Это соответствует системе:
\[
y = x^2, \quad y = 4x — 3.
\]

Решим исходное уравнение:
\[
x^2 — 4x + 3 = 0.
\]

Дискриминант:
\[
D = (-4)^2 — 4 \cdot 1 \cdot 3 = 16 — 12 = 4.
\]

Корни:
\[
x = \frac{4 \pm \sqrt{4}}{2} = \frac{4 \pm 2}{2}.
\]

Получаем:
— \(x_1 = \frac{4 + 2}{2} = 3\),
— \(x_2 = \frac{4 — 2}{2} = 1\).

Проверка:
— При \(x = 3\): \(9 — 12 = -3\) — верно.
— При \(x = 1\): \(1 — 4 = -3\) — верно.

Ответ: \(x = 1,\ x = 3\).

в) \(x^2 + 4x + 3 = 0\)

Выразим \(x^2\):
\[
x^2 = -4x — 3.
\]

Система функций:
\[
y = x^2, \quad y = -4x — 3.
\]

Решим квадратное уравнение:
\[
x^2 + 4x + 3 = 0.
\]

Можно разложить на множители:
\[
(x + 1)(x + 3) = 0,
\]

откуда \(x = -1\) или \(x = -3\).

Или через дискриминант:
\[
D = 4^2 — 4 \cdot 1 \cdot 3 = 16 — 12 = 4,
\]

\[
x = \frac{-4 \pm 2}{2} \Rightarrow x = -1,\ x = -3.
\]

Проверка:
— При \(x = -1\): \(1 — 4 + 3 = 0\) — верно.
— При \(x = -3\): \(9 — 12 + 3 = 0\) — верно.

Ответ: \(x = -3,\ x = -1\).

г) \(x^2 — x = 6\)

Переносим 6 влево или выражаем \(x^2\):
\[
x^2 = x + 6.
\]

Система:
\[
y = x^2, \quad y = x + 6.
\]

Приведём к стандартному виду:
\[
x^2 — x — 6 = 0.
\]

Разложим на множители:
\[
(x — 3)(x + 2) = 0,
\]

откуда \(x = 3\) или \(x = -2\).

Через дискриминант:
\[
D = (-1)^2 — 4 \cdot 1 \cdot (-6) = 1 + 24 = 25,
\]

\[
x = \frac{1 \pm 5}{2} \Rightarrow x = 3,\ x = -2.
\]

Проверка:
— При \(x = 3\): \(9 — 3 = 6\) — верно.
— При \(x = -2\): \(4 — (-2) = 4 + 2 = 6\) — верно.

Ответ: \(x = -2,\ x = 3\).