ГДЗ по Алгебре 7 Класс Номер 46.14 Мордкович — Подробные Ответы

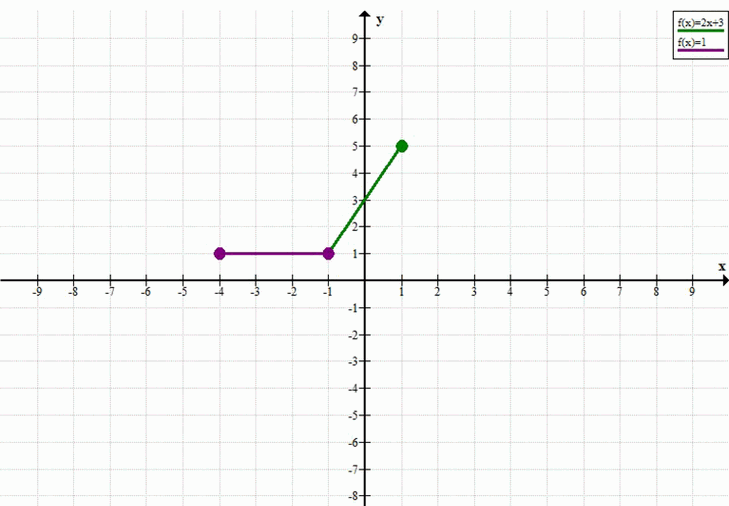
Постройте график функции: а) y= система 1, если -4 ≤ х ≤ -1; 2х + 3, если -1 < х ≤ 1; б) y=система 0, если -5 ≤ х ≤ -2; х + 2, если -2 < х ≤ 2.

а)
\( y = \begin{cases} 1, & \text{если } -4 \le x \le -1 \\ 2x + 3, & \text{если } -1 < x \le 1 \end{cases} \)
Построим график функции по частям.
Первая часть: \( y = 1 \) при \( -4 \le x \le -1 \).
Это горизонтальный отрезок прямой.
Начальная точка: \( x = -4 \Rightarrow y = 1 \). Точка \((-4, 1)\) (включена).
Конечная точка: \( x = -1 \Rightarrow y = 1 \). Точка \((-1, 1)\) (включена).
Вторая часть: \( y = 2x + 3 \) при \( -1 < x \le 1 \).
Это отрезок прямой.
Начальная точка: \( x = -1 \Rightarrow y = 2(-1) + 3 = -2 + 3 = 1 \). Точка \((-1, 1)\) (не включена, но совпадает с конечной точкой первого отрезка, поэтому будет сплошной).
Конечная точка: \( x = 1 \Rightarrow y = 2(1) + 3 = 2 + 3 = 5 \). Точка \((1, 5)\) (включена).

Ответ: График состоит из двух отрезков: первый отрезок соединяет точки \((-4, 1)\) и \((-1, 1)\), второй отрезок соединяет точки \((-1, 1)\) и \((1, 5)\).

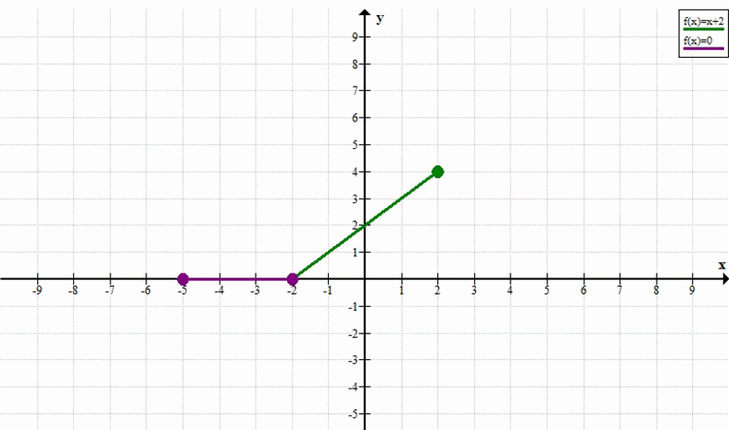
б)
\( y = \begin{cases} 0, & \text{если } -5 \le x \le -2 \\ x + 2, & \text{если } -2 < x \le 2 \end{cases} \)
Построим график функции по частям.
Первая часть: \( y = 0 \) при \( -5 \le x \le -2 \).
Это горизонтальный отрезок прямой, лежащий на оси абсцисс.
Начальная точка: \( x = -5 \Rightarrow y = 0 \). Точка \((-5, 0)\) (включена).
Конечная точка: \( x = -2 \Rightarrow y = 0 \). Точка \((-2, 0)\) (включена).
Вторая часть: \( y = x + 2 \) при \( -2 < x \le 2 \).
Это отрезок прямой.
Начальная точка: \( x = -2 \Rightarrow y = -2 + 2 = 0 \). Точка \((-2, 0)\) (не включена, но совпадает с конечной точкой первого отрезка, поэтому будет сплошной).
Конечная точка: \( x = 2 \Rightarrow y = 2 + 2 = 4 \). Точка \((2, 4)\) (включена).

Ответ: График состоит из двух отрезков: первый отрезок соединяет точки \((-5, 0)\) и \((-2, 0)\), второй отрезок соединяет точки \((-2, 0)\) и \((2, 4)\).

Условие: Постройте график функции:

а)
\(y= \begin{cases} 1, & \text{если } -4 \le x \le -1 \\ 2x + 3, & \text{если } -1 < x \le 1 \end{cases}\);

б)
\(y= \begin{cases} 0, & \text{если } -5 \le x \le -2 \\ x + 2, & \text{если } -2 < x \le 2 \end{cases}\)

Решение:
Для построения графика кусочно-заданной функции необходимо построить график каждой части функции на соответствующем интервале.

а) Функция \(y= \begin{cases} 1, & \text{если } -4 \le x \le -1 \\ 2x + 3, & \text{если } -1 < x \le 1 \end{cases}\)

Построение первой части графика: \(y = 1\) при \( -4 \le x \le -1 \).
Это горизонтальный отрезок прямой.
Вычислим значения на границах интервала:
При \( x = -4 \), \( y = 1 \). Отмечаем точку \( (-4, 1) \). Эта точка включена в график (закрашенная).
При \( x = -1 \), \( y = 1 \). Отмечаем точку \( (-1, 1) \). Эта точка включена в график (закрашенная).
Начертите отрезок прямой, соединяющий точки \( (-4, 1) \) и \( (-1, 1) \).

Построение второй части графика: \(y = 2x + 3\) при \( -1 < x \le 1 \).
Это отрезок прямой.
Вычислим значения на границах интервала:
При \( x = -1 \), \( y = 2(-1) + 3 = -2 + 3 = 1 \). Отмечаем точку \( (-1, 1) \). Согласно условию \( -1 < x \), эта точка не включена в график для данной части (открытая точка).
При \( x = 1 \), \( y = 2(1) + 3 = 2 + 3 = 5 \). Отмечаем точку \( (1, 5) \). Эта точка включена в график (закрашенная).
Начертите отрезок прямой, соединяющий точку \( (-1, 1) \) (открытая) и \( (1, 5) \) (закрашенная).
Обратите внимание, что в точке \( x = -1 \) значение первой части функции \( y = 1 \) (включено) и значение второй части функции \( y = 1 \) (не включено). Таким образом, точка \( (-1, 1) \) будет закрашенной на итоговом графике, обеспечивая непрерывность.

б) Функция \(y= \begin{cases} 0, & \text{если } -5 \le x \le -2 \\ x + 2, & \text{если } -2 < x \le 2 \end{cases}\)

Построение первой части графика: \(y = 0\) при \( -5 \le x \le -2 \).
Это горизонтальный отрезок прямой, лежащий на оси абсцисс.
Вычислим значения на границах интервала:
При \( x = -5 \), \( y = 0 \). Отмечаем точку \( (-5, 0) \). Эта точка включена в график (закрашенная).
При \( x = -2 \), \( y = 0 \). Отмечаем точку \( (-2, 0) \). Эта точка включена в график (закрашенная).
Начертите отрезок прямой, соединяющий точки \( (-5, 0) \) и \( (-2, 0) \).

Построение второй части графика: \(y = x + 2\) при \( -2 < x \le 2 \).
Это отрезок прямой.
Вычислим значения на границах интервала:
При \( x = -2 \), \( y = -2 + 2 = 0 \). Отмечаем точку \( (-2, 0) \). Согласно условию \( -2 < x \), эта точка не включена в график для данной части (открытая точка).
При \( x = 2 \), \( y = 2 + 2 = 4 \). Отмечаем точку \( (2, 4) \). Эта точка включена в график (закрашенная).
Начертите отрезок прямой, соединяющий точку \( (-2, 0) \) (открытая) и \( (2, 4) \) (закрашенная).
Обратите внимание, что в точке \( x = -2 \) значение первой части функции \( y = 0 \) (включено) и значение второй части функции \( y = 0 \) (не включено). Таким образом, точка \( (-2, 0) \) будет закрашенной на итоговом графике, обеспечивая непрерывность.

Ответ: Графики функций построены согласно описанным шагам.