ГДЗ по Алгебре 7 Класс Номер 46.17 Мордкович — Подробные Ответы

Постройте график функции: а) y= система \(x^2\), если -3 ≤ х ≤ 0; х, если 0 ≤ х ≤ 4; б) y=система -x, если -4 ≤ х < 0; \(-x^2\), если 0 ≤ х ≤ 2.

а)
\( y = \begin{cases} x^2, & \text{если } -3 \le x \le 0 \\ x, & \text{если } 0 \le x \le 4 \end{cases} \)
\( y(-3) = (-3)^2 = 9 \)
\( y(0) = (0)^2 = 0 \)
\( y(4) = 4 \)

Ответ: \( \{ (x, x^2) \mid -3 \le x \le 0 \} \cup \{ (x, x) \mid 0 \le x \le 4 \} \)

б)
\( y = \begin{cases} -x, & \text{если } -4 \le x < 0 \\ -x^2, & \text{если } 0 \le x \le 2 \end{cases} \)
\( y(-4) = -(-4) = 4 \)
\( \lim_{x \to 0^-} y(x) = \lim_{x \to 0^-} (-x) = 0 \)
\( y(0) = -(0)^2 = 0 \)
\( y(2) = -(2)^2 = -4 \)

Ответ: \( \{ (x, -x) \mid -4 \le x < 0 \} \cup \{ (x, -x^2) \mid 0 \le x \le 2 \} \)

Условие: Постройте график функции:

а)
\(y= \begin{cases} x^2, & \text{если } -3 \le x \le 0 \\ x, & \text{если } 0 < x \le 4 \end{cases}\);

б)
\(y= \begin{cases} -x, & \text{если } -4 \le x < 0 \\ -x^2, & \text{если } 0 \le x \le 2 \end{cases}\)

Решение:
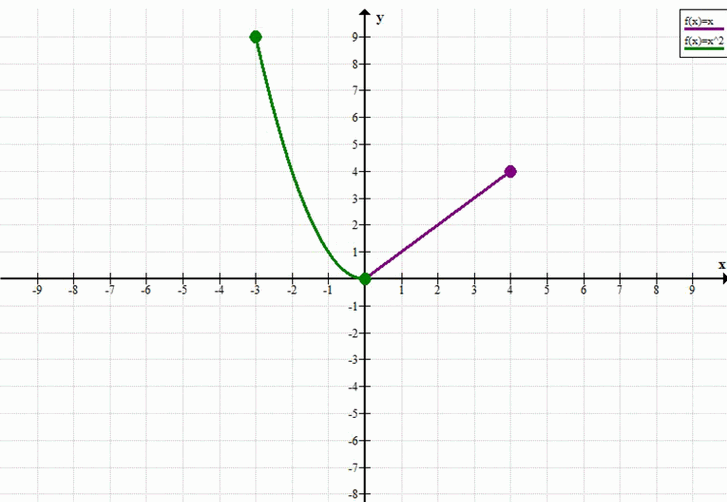
а) Построение графика функции \(y= \begin{cases} x^2, & \text{если } -3 \le x \le 0 \\ x, & \text{если } 0 < x \le 4 \end{cases}\):
График состоит из двух частей.

Первая часть: \(y = x^2\) при \(x \in [-3, 0]\).
Это часть параболы, ветви которой направлены вверх, с вершиной в точке \((0, 0)\).
Вычислим значения функции на концах интервала:
При \(x = -3\), \(y = (-3)^2 = 9\). Отметим точку \((-3, 9)\).
При \(x = 0\), \(y = (0)^2 = 0\). Отметим точку \((0, 0)\).
Соединим эти точки плавной кривой, соответствующей параболе \(y = x^2\).

Вторая часть: \(y = x\) при \(x \in (0, 4]\).
Это часть прямой линии, проходящей через начало координат с угловым коэффициентом 1.
Вычислим значения функции на концах интервала:
При \(x = 0\), \(y = 0\). Эта точка \((0, 0)\) является началом отрезка, но не включается в интервал для этой части функции. Однако, поскольку она включена в первую часть, она будет закрашенной.
При \(x = 4\), \(y = 4\). Отметим точку \((4, 4)\).
Соединим точки \((0, 0)\) и \((4, 4)\) отрезком прямой.

Таким образом, график функции состоит из параболического отрезка от \((-3, 9)\) до \((0, 0)\) и линейного отрезка от \((0, 0)\) до \((4, 4)\).

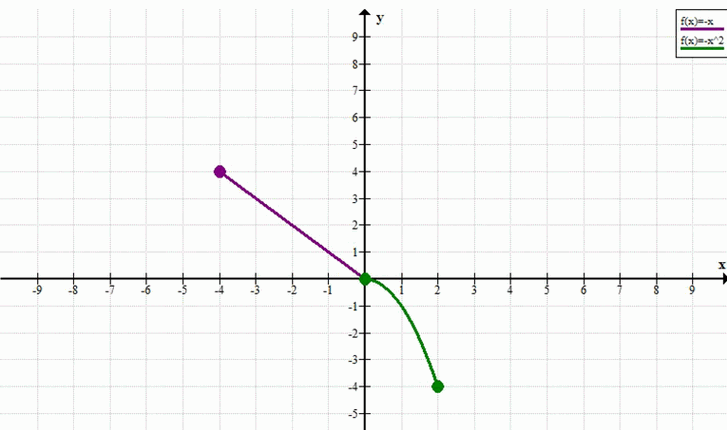
б) Построение графика функции \(y= \begin{cases} -x, & \text{если } -4 \le x < 0 \\ -x^2, & \text{если } 0 \le x \le 2 \end{cases}\):
График состоит из двух частей.

Первая часть: \(y = -x\) при \(x \in [-4, 0)\).
Это часть прямой линии, проходящей через начало координат с угловым коэффициентом -1.
Вычислим значения функции на концах интервала:
При \(x = -4\), \(y = -(-4) = 4\). Отметим точку \((-4, 4)\).
При \(x = 0\), \(y = -(0) = 0\). Отметим точку \((0, 0)\). Эта точка не включается в интервал для этой части функции, поэтому она будет обозначена «выколотой» (пустой) точкой.
Соединим точки \((-4, 4)\) и \((0, 0)\) отрезком прямой.

Вторая часть: \(y = -x^2\) при \(x \in [0, 2]\).
Это часть параболы, ветви которой направлены вниз, с вершиной в точке \((0, 0)\).
Вычислим значения функции на концах интервала:
При \(x = 0\), \(y = -(0)^2 = 0\). Отметим точку \((0, 0)\). Эта точка включается в интервал для этой части функции, поэтому она «закрашивает» выколотую точку из первой части.
При \(x = 2\), \(y = -(2)^2 = -4\). Отметим точку \((2, -4)\).
Соединим точки \((0, 0)\) и \((2, -4)\) плавной кривой, соответствующей параболе \(y = -x^2\).

Таким образом, график функции состоит из линейного отрезка от \((-4, 4)\) до \((0, 0)\) и параболического отрезка от \((0, 0)\) до \((2, -4)\).

Ответ: Графики функций строятся согласно приведенному описанию.