Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 46.19 Мордкович — Подробные Ответы
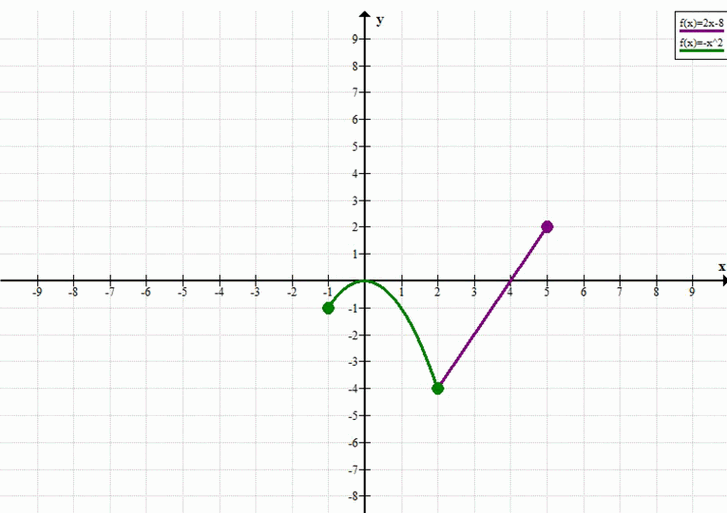
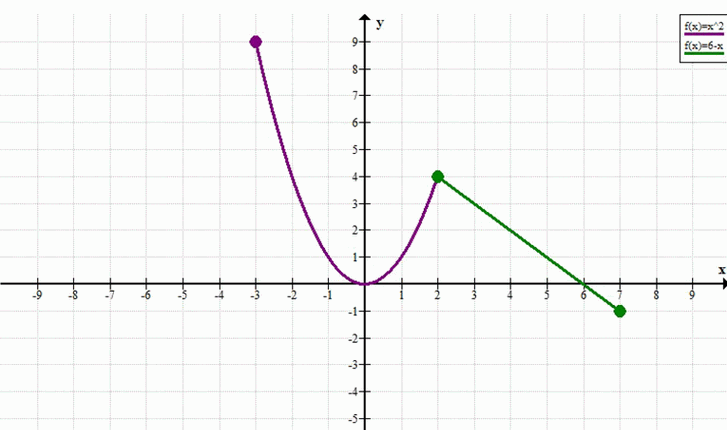
а) y= система \(-x^2\), если -1 < = х ≤ 2; 2х-8, если 2 < х ≤ 5; б) y=система \(x^2\), если -3 ≤ х < 2; 6-x, если 2 < = х ≤ 7.
а)
\( D_1 = [-1, 2] \)
\( D_2 = (2, 5] \)
\( D = D_1 \cup D_2 \)
\( D = [-1, 5] \)
б)
\( D_1 = [-3, 2) \)
\( D_2 = [2, 7] \)
\( D = D_1 \cup D_2 \)
\( D = [-3, 7] \)
Условие: Дана кусочно-заданная функция \( y \):
\( y = \begin{cases} -x^2, & \text{если } -1 \le x \le 2 \\ 2x — 8, & \text{если } 2 < x \le 5 \end{cases} \)
Найти значение функции в точке \( x = 2 \).
Решение:
Для нахождения значения функции в точке \( x = 2 \), необходимо определить, к какому интервалу принадлежит данное значение \( x \).
Значение \( x = 2 \) удовлетворяет условию первого интервала: \( -1 \le x \le 2 \).
Следовательно, для вычисления \( y \) используем первое правило функции: \( y = -x^2 \).
Подставим \( x = 2 \) в соответствующее выражение:
\( y = -(2)^2 \)
Вычислим значение:
\( y = -4 \)
Ответ: -4
Условие: Дана кусочно-заданная функция \( y \):
\( y = \begin{cases} x^2, & \text{если } -3 \le x < 2 \\ 6 — x, & \text{если } 2 \le x \le 7 \end{cases} \)
Найти значение функции в точке \( x = 2 \).
Решение:
Для нахождения значения функции в точке \( x = 2 \), необходимо определить, к какому интервалу принадлежит данное значение \( x \).
Значение \( x = 2 \) удовлетворяет условию второго интервала: \( 2 \le x \le 7 \).
Следовательно, для вычисления \( y \) используем второе правило функции: \( y = 6 — x \).
Подставим \( x = 2 \) в соответствующее выражение:
\( y = 6 — 2 \)
Вычислим значение:
\( y = 4 \)
Ответ: 4