ГДЗ по Алгебре 7 Класс Номер 46.20 Мордкович — Подробные Ответы

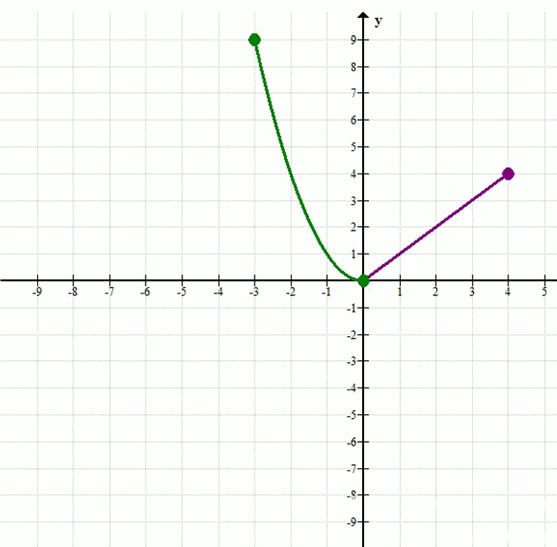
Для функций из упражнения 39.17 а) найдите: а) значения функции при значении аргумента, равном -1; 0; 2; 4; б) значения аргумента, если значение функции равно 0; 1; 4; в) наибольшее и наименьшее значения функции на отрезке [-1; 2]; г) промежутки возрастания и убывания функции.

\(y =
\begin{cases}
x^2, & -3 \leq x \leq 0 \\
x, & 0 < x \leq 4
\end{cases}\)

а) \(x = -1,\quad y = 1;\)
\(x = 0,\quad y = 0;\)
\(x = 2,\quad y = 2;\)
\(x = 4,\quad y = 4.\)

б) \(y = 0,\quad x = 0;\)
\(y = 1,\quad x = \pm 1;\)
\(y = 4,\quad x = -2,\ x = 4.\)

в) \([-1; 2] — y_{\text{наим}} = 0,\quad y_{\text{наиб}} = 2.\)

г) функция возрастает при \(x \in [0; 4]\), функция убывает при \(x \in [-3; 0]\).

Дана кусочная функция:

\[
y =
\begin{cases}
x^2, & -3 \leq x \leq 0, \\
x, & 0 < x \leq 4.
\end{cases}
\]

Эта функция состоит из двух частей:
— На отрезке \([-3; 0]\) — это квадратичная функция \(y = x^2\), график которой — часть параболы, ветви направлены вверх, вершина в точке \((0; 0)\).
— На полуинтервале \((0; 4]\) — это линейная функция \(y = x\), график которой — отрезок прямой под углом 45° к оси абсцисс.

Важно отметить, что в точке \(x = 0\) функция определена только первой формулой (поскольку вторая начинается с \(0 < x\)). При этом \(f(0) = 0^2 = 0\), а предел справа также равен 0, поэтому функция непрерывна в этой точке, несмотря на смену формулы.

Рассмотрим каждый пункт подробно.

а) Найдём значения функции в заданных точках

— \(x = -1\)
Так как \(-3 \leq -1 \leq 0\), используем первую формулу:
\(y = (-1)^2 = 1\).

— \(x = 0\)
Точка \(x = 0\) входит в первый промежуток (\(-3 \leq x \leq 0\)), поэтому:
\(y = 0^2 = 0\).

— \(x = 2\)
Так как \(0 < 2 \leq 4\), используем вторую формулу:
\(y = 2\).

— \(x = 4\)
Точка \(x = 4\) входит во второй промежуток, поэтому:
\(y = 4\).

Все вычисления подтверждают корректность выбора формулы в зависимости от промежутка.

б) Найдём значения аргумента \(x\), при которых функция принимает заданные значения

— \(y = 0\)
Рассмотрим обе части:
— В первой части: \(x^2 = 0 \Rightarrow x = 0\) (и \(0 \in [-3; 0]\) — допустимо).
— Во второй части: \(x = 0\), но \(x = 0\) не входит в \((0; 4]\).
Следовательно, единственное решение: \(x = 0\).

— \(y = 1\)
— В первой части: \(x^2 = 1 \Rightarrow x = \pm 1\). Но только \(x = -1\) принадлежит \([-3; 0]\) (так как \(1 > 0\)).
— Во второй части: \(x = 1\), и \(1 \in (0; 4]\) — допустимо.
Итого: \(x = -1\) и \(x = 1\), то есть \(x = \pm 1\).

— \(y = 4\)
— В первой части: \(x^2 = 4 \Rightarrow x = \pm 2\). Из них только \(x = -2\) принадлежит \([-3; 0]\).
— Во второй части: \(x = 4\), и \(4 \in (0; 4]\) — допустимо.
Итого: \(x = -2\) и \(x = 4\).

Эти решения демонстрируют, как одна и та же ордината может соответствовать разным абсциссам из разных частей графика.

в) Найдём наименьшее и наибольшее значения функции на отрезке \([-1; 2]\)

Разобьём отрезок на две части в соответствии с определением функции:
— На \([-1; 0]\): \(y = x^2\),
— На \((0; 2]\): \(y = x\).

Анализируем каждую часть:

— На \([-1; 0]\):
Функция \(y = x^2\) убывает (так как мы движемся слева направо к вершине).
Значения: от \(y(-1) = 1\) до \(y(0) = 0\).

— На \((0; 2]\):
Функция \(y = x\) возрастает.
Значения: от \(y \to 0^+\) до \(y(2) = 2\).

Объединяя обе части, получаем:
— Минимальное значение: \(y = 0\) (достигается в \(x = 0\)),
— Максимальное значение: \(y = 2\) (достигается в \(x = 2\)).

Ответ: \(y_{\text{наим}} = 0,\ y_{\text{наиб}} = 2\).

г) Определим промежутки возрастания и убывания функции

— На \([-3; 0]\):
Функция \(y = x^2\).
Поскольку мы находимся левее вершины параболы, функция убывает при движении от \(-3\) к \(0\).

— На \((0; 4]\):
Функция \(y = x\) — линейная с положительным угловым коэффициентом, поэтому возрастает.

Точка \(x = 0\) является общей границей. Хотя в ней происходит смена формулы, поведение функции согласовано: слева — убывание к нулю, справа — возрастание от нуля.

Следовательно:
— Функция убывает на \([-3; 0]\),
— Функция возрастает на \([0; 4]\) (включая 0, так как в этой точке достигается минимум).