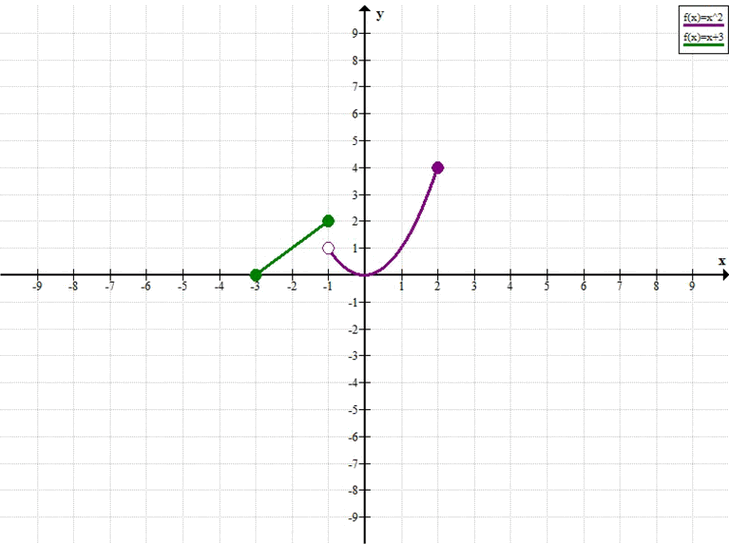ГДЗ по Алгебре 7 Класс Номер 46.21 Мордкович — Подробные Ответы

Для функций из упражнения 39.18 а) найдите: а) область определения; б) наименьшее и наибольшее значения; в) промежутки убывания и возрастания; г) точки разрыва.

\(y =
\begin{cases}
x + 3, & -3 \leq x \leq -1 \\
x^2, & -1 < x \leq 2
\end{cases}\)

а) Область определения: \([-3; 2]\).

б) \(y_{\text{наим}} = 0,\quad y_{\text{наиб}} = 4.\)

в) функция возрастает при \(x \in [-3; -1]\) и \([0; 2]\);
убывает при \(x \in (-1; 0)\).

г) точка разрыва при \(x = -1\).

а) Область определения: \([-3; 2]\)

Область определения — это множество всех значений \(x\), при которых функция имеет смысл.

— Первая часть задана на \([-3; -1]\) — включает оба конца.
— Вторая часть — на \((-1; 2]\) — не включает \(-1\), но включает \(2\).

Объединяя эти два промежутка, получаем:
\[
[-3; -1] \cup (-1; 2] = [-3; 2].
\]

Точка \(x = -1\) покрыта первой частью, поэтому в итоговом промежутке нет «дыры» — область определения — сплошной отрезок от \(-3\) до \(2\).

Ответ: \([-3; 2]\).

б) Наименьшее и наибольшее значения: \(y_{\text{наим}} = 0,\ y_{\text{наиб}} = 4\)**

Найдём экстремумы на каждом участке.

1. На \([-3; -1]\):
Функция \(y = x + 3\) — возрастающая прямая.
— При \(x = -3\): \(y = -3 + 3 = 0\),
— При \(x = -1\): \(y = -1 + 3 = 2\).
Значения на этом участке: от \(0\) до \(2\).

2. На \((-1; 2]\):
Функция \(y = x^2\) — парабола, ветви вверх, вершина в \(x = 0\).
— При \(x \to -1^{+}\): \(y \to (-1)^2 = 1\), но значение \(y = 1\) не достигается, так как \(x = -1\) не входит в этот промежуток.
— При \(x = 0\): \(y = 0\) — минимум.
— При \(x = 2\): \(y = 4\) — максимум.

Сравниваем все возможные значения:
— Наименьшее: \(0\) (достигается и при \(x = -3\), и при \(x = 0\)),
— Наибольшее: \(4\) (при \(x = 2\)).

Ответ: \(y_{\text{наим}} = 0,\ y_{\text{наиб}} = 4\).

в) Промежутки возрастания и убывания

Анализируем каждую часть:

— \(y = x + 3\) на \([-3; -1]\) — линейная функция с положительным угловым коэффициентом → возрастает на всём отрезке.

— \(y = x^2\) на \((-1; 2]\) — парабола:
— Убывает на \((-1; 0)\) (левая ветвь),
— Возрастает на \([0; 2]\) (правая ветвь).

Объединяя:
— Функция возрастает на \([-3; -1]\) и \([0; 2]\),
— Убывает на \((-1; 0)\).

Обратите внимание: в точке \(x = -1\) происходит переход от линейной части к параболе, но поскольку \(x = -1\) не входит во вторую часть, интервал убывания начинается строго после \(-1\).

г) Точка разрыва при \(x = -1\)

Проверим непрерывность в точке \(x = -1\):

— Значение функции:
\(f(-1) = -1 + 3 = 2\) (по первой формуле).

— Предел справа:
\(\lim_{x \to -1^{+}} f(x) = \lim_{x \to -1^{+}} x^2 = 1\).

— Предел слева:
\(\lim_{x \to -1^{-}} f(x) = \lim_{x \to -1^{-}} (x + 3) = 2\).

Поскольку предел справа (\(1\)) не равен значению функции (\(2\)), функция разрывна в точке \(x = -1\). Это скачок величиной \(1\).

Таким образом, \(x = -1\) — точка разрыва первого рода (конечный скачок).