ГДЗ по Алгебре 7 Класс Номер 46.27 Мордкович — Подробные Ответы

Дана функция у = f(x), где f(x) = система 2-х, если -4 ≤ х < -2; x², если -2 ≤ х ≤ 2; 0,5х + 3, если 2 < х ≤ 4. а) Вычислите f(-4), f(-2), f(1), f(4). б) Постройте график функции у = f(x). в) С помощью графика найдите значения аргумента, если fix) = 1, fix) = 0, fix) = 5, fix) = 6

f(x) =
{ 2 — x, -4 ≤ x < -2
x², -2 ≤ x ≤ 2
0,5x + 3, 2 < x ≤ 4

а) f(-4) = 2 — (-4) = 2 + 4 = 6.
f(-2) = (-2)² = 4.
f(1) = 1² = 1.
f(4) = 0,5 · 4 + 3 = 2 + 3 = 5.

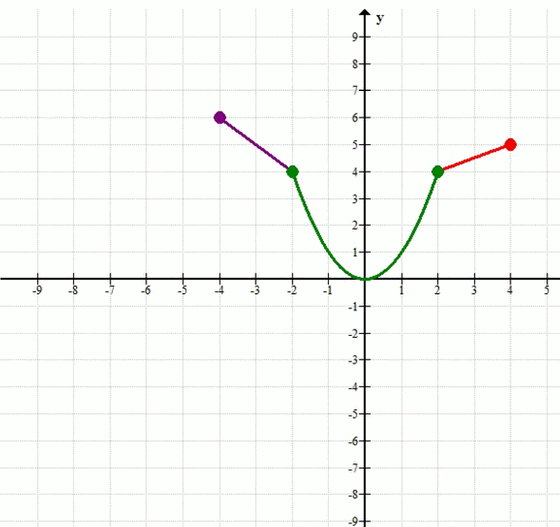
б) y = f(x)

в) f(x) = 1 ⇒ y = 1, x = ±1;
f(x) = 0 ⇒ y = 0, x = 0;
f(x) = 5 ⇒ y = 5, x = -3, x = 4;
f(x) = 6 ⇒ y = 6, x = -4.

а) Вычисление значений функции

1. \(f(-4)\)
Проверяем: \(-4 \in [-4; -2)\) — да.
Используем первую формулу: \(f(x) = 2 — x\).
\[
f(-4) = 2 — (-4) = 2 + 4 = 6.
\]

2. \(f(-2)\)
Проверяем: \(-2 \in [-2; 2]\) — да (вторая часть).
Используем \(f(x) = x^2\):
\[
f(-2) = (-2)^2 = 4.
\]

3. \(f(1)\)
\(1 \in [-2; 2]\) — да.
\[
f(1) = 1^2 = 1.
\]

4. \(f(4)\)
\(4 \in (2; 4]\) — да.
Используем третью формулу: \(f(x) = 0{,}5x + 3\).
\[
f(4) = 0{,}5 \cdot 4 + 3 = 2 + 3 = 5.
\]

Все вычисления подтверждают правильный выбор формулы.

б) График функции \(y = f(x)\)

Хотя график не приводится, опишем его ключевые особенности:

— На \([-4; -2)\): отрезок прямой от точки \((-4; 6)\) до \((-2; 4)\), причём точка \((-2; 4)\) не включена (пустая точка).
— На \([-2; 2]\): парабола от \((-2; 4)\) через \((0; 0)\) до \((2; 4)\), обе концевые точки включены.
-На \((2; 4]\): отрезок прямой от \((2; 4)\) (не включена) до \((4; 5)\) (включена).

В точках \(x = -2\) и \(x = 2\) функция непрерывна, так как пределы слева и справа совпадают со значением функции.

в) Решение уравнений вида \(f(x) = c\)

Решаем, при каких \(x\) функция принимает заданное значение.

1. \(f(x) = 1\)
Рассмотрим каждую часть:

— Первая: \(2 — x = 1 \Rightarrow x = 1\), но \(1 \notin [-4; -2)\) — не подходит.
— Вторая: \(x^2 = 1 \Rightarrow x = \pm 1\), оба значения в \([-2; 2]\) — подходят.
— Третья: \(0{,}5x + 3 = 1 \Rightarrow 0{,}5x = -2 \Rightarrow x = -4\), но \(-4 \notin (2; 4]\) — не подходит.

Ответ: \(x = -1,\ x = 1\).

2. \(f(x) = 0\)
— Первая: \(2 — x = 0 \Rightarrow x = 2\), но \(2 \notin [-4; -2)\) — нет.
— Вторая: \(x^2 = 0 \Rightarrow x = 0 \in [-2; 2]\) — подходит.
— Третья: \(0{,}5x + 3 = 0 \Rightarrow x = -6 \notin (2; 4]\) — нет.

Ответ: \(x = 0\).

3. \(f(x) = 5\)
— Первая: \(2 — x = 5 \Rightarrow x = -3\). Проверяем: \(-3 \in [-4; -2)\) — да.
— Вторая: \(x^2 = 5 \Rightarrow x = \pm\sqrt{5} \approx \pm2{,}24\), но \(|x| > 2\) — не входит в \([-2; 2]\).
— Третья: \(0{,}5x + 3 = 5 \Rightarrow 0{,}5x = 2 \Rightarrow x = 4 \in (2; 4]\) — да.

Ответ: \(x = -3,\ x = 4\).

4. \(f(x) = 6\)
— Первая: \(2 — x = 6 \Rightarrow x = -4 \in [-4; -2)\) — да.
— Вторая: \(x^2 = 6 \Rightarrow x = \pm\sqrt{6} \approx \pm2{,}45\), не в \([-2; 2]\).
— Третья: \(0{,}5x + 3 = 6 \Rightarrow x = 6 \notin (2; 4]\).

Ответ: \(x = -4\).

Итоговые ответы:

а)
— \(f(-4) = 6\),
— \(f(-2) = 4\),
— \(f(1) = 1\),
— \(f(4) = 5\).

б) График состоит из трёх участков: линейного, параболического и линейного.

в)
— \(f(x) = 1\) при \(x = \pm1\),
— \(f(x) = 0\) при \(x = 0\),
— \(f(x) = 5\) при \(x = -3\) и \(x = 4\),
— \(f(x) = 6\) при \(x = -4\).