ГДЗ по Алгебре 7 Класс Номер 46.28 Мордкович — Подробные Ответы

Дана функция у = f(x), где f(x) = система х+2, если х < -1; x², если -1 ≤ х ≤ 2; х + 2, если x > 2. а) Вычислите f(0), f(-2), f(2), f(3). б) Постройте график функции у = f(x). в) С помощью графика найдите значения аргумента, если f(x) = 1, f(x) = 0, f(x) = 4, f(х) = -1.

f(x) =
{ x + 2, x < -1
x², -1 ≤ x ≤ 2
x + 2, x > 2

а) f(0) = 0² = 0.
f(-2) = -2 + 2 = 0.
f(2) = 2 + 2 = 4.
f(3) = 3 + 2 = 5.

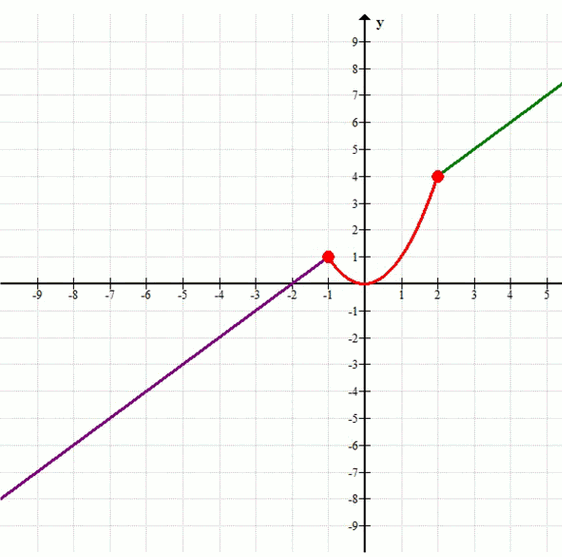
б) y = f(x)

в) f(x) = 1 ⇒ y = 1, x = ±1;
f(x) = 0 ⇒ y = 0, x = -2, x = 0;
f(x) = 4 ⇒ y = 4, x = 2;
f(x) = -1 ⇒ y = -1, x = -3.

Условие: Дана функция \(у = f(x), где f(x) = \begin{cases} x+2, & \text{если } x < -1 \\ x^2, & \text{если } -1 \le x \le 2 \\ x+2, & \text{если } x > 2 \end{cases}\).

а) Вычислите \(f(0), f(-2), f(2), f(3)\).

б) Постройте график функции \(у = f(x)\).

в) С помощью графика найдите значения аргумента, если \(f(x) = 1, f(x) = 0, f(x) = 4, f(х) = -1\).

Решение:
а) Вычислим значения функции для заданных аргументов:

Для \(f(0)\):
Аргумент \(x = 0\) находится в интервале \( -1 \le x \le 2 \).
Используем формулу \(f(x) = x^2\).
\(f(0) = 0^2\)
\(f(0) = 0\)

Для \(f(-2)\):
Аргумент \(x = -2\) находится в интервале \( x < -1 \).
Используем формулу \(f(x) = x+2\).
\(f(-2) = -2+2\)
\(f(-2) = 0\)

Для \(f(2)\):
Аргумент \(x = 2\) находится в интервале \( -1 \le x \le 2 \).
Используем формулу \(f(x) = x^2\).
\(f(2) = 2^2\)
\(f(2) = 4\)

Для \(f(3)\):
Аргумент \(x = 3\) находится в интервале \( x > 2 \).
Используем формулу \(f(x) = x+2\).
\(f(3) = 3+2\)
\(f(3) = 5\)

б) Построим график функции \(у = f(x)\).
График функции состоит из трех частей:
1. Для \(x < -1\): График представляет собой часть прямой \(y = x+2\).
Например, при \(x = -2\), \(y = 0\). При \(x = -1\) (не включая), \(y = 1\).
Этот участок является открытым лучом, заканчивающимся «выколотой» точкой \( (-1, 1) \).
2. Для \( -1 \le x \le 2 \): График представляет собой часть параболы \(y = x^2\).
Например, при \(x = -1\), \(y = (-1)^2 = 1\).
При \(x = 0\), \(y = 0^2 = 0\).
При \(x = 1\), \(y = 1^2 = 1\).
При \(x = 2\), \(y = 2^2 = 4\).
Этот участок является отрезком параболы, включающим точки \( (-1, 1) \) и \( (2, 4) \).
3. Для \(x > 2\): График представляет собой часть прямой \(y = x+2\).
Например, при \(x = 3\), \(y = 5\). При \(x = 2\) (не включая), \(y = 4\).
Этот участок является открытым лучом, начинающимся «выколотой» точкой \( (2, 4) \).

в) С помощью графика найдем значения аргумента для заданных значений функции. Это эквивалентно решению уравнений \(f(x) = C\).

1. Если \(f(x) = 1\):
Рассмотрим каждый участок функции:
Случай 1: \(x+2 = 1\) для \(x < -1\).
\(x = 1 — 2\)
\(x = -1\)
Значение \(x = -1\) не удовлетворяет условию \(x < -1\). Решений нет на этом участке.
Случай 2: \(x^2 = 1\) для \( -1 \le x \le 2 \).
\(x = \pm \sqrt{1}\)
\(x = 1\) или \(x = -1\)
Оба значения \(x = 1\) и \(x = -1\) удовлетворяют условию \( -1 \le x \le 2 \).
Случай 3: \(x+2 = 1\) для \(x > 2\).
\(x = 1 — 2\)
\(x = -1\)
Значение \(x = -1\) не удовлетворяет условию \(x > 2\). Решений нет на этом участке.
Таким образом, при \(f(x) = 1\), значения аргумента: \(x = -1\) и \(x = 1\).

2. Если \(f(x) = 0\):
Рассмотрим каждый участок функции:
Случай 1: \(x+2 = 0\) для \(x < -1\).
\(x = -2\)
Значение \(x = -2\) удовлетворяет условию \(x < -1\).
Случай 2: \(x^2 = 0\) для \( -1 \le x \le 2 \).
\(x = 0\)
Значение \(x = 0\) удовлетворяет условию \( -1 \le x \le 2 \).
Случай 3: \(x+2 = 0\) для \(x > 2\).
\(x = -2\)
Значение \(x = -2\) не удовлетворяет условию \(x > 2\). Решений нет на этом участке.
Таким образом, при \(f(x) = 0\), значения аргумента: \(x = -2\) и \(x = 0\).

3. Если \(f(x) = 4\):
Рассмотрим каждый участок функции:
Случай 1: \(x+2 = 4\) для \(x < -1\).
\(x = 4 — 2\)
\(x = 2\)
Значение \(x = 2\) не удовлетворяет условию \(x < -1\). Решений нет на этом участке.
Случай 2: \(x^2 = 4\) для \( -1 \le x \le 2 \).
\(x = \pm \sqrt{4}\)
\(x = 2\) или \(x = -2\)
Значение \(x = 2\) удовлетворяет условию \( -1 \le x \le 2 \).
Значение \(x = -2\) не удовлетворяет условию \( -1 \le x \le 2 \).
Случай 3: \(x+2 = 4\) для \(x > 2\).
\(x = 4 — 2\)
\(x = 2\)
Значение \(x = 2\) не удовлетворяет условию \(x > 2\). Решений нет на этом участке.
Таким образом, при \(f(x) = 4\), значение аргумента: \(x = 2\).

4. Если \(f(x) = -1\):
Рассмотрим каждый участок функции:
Случай 1: \(x+2 = -1\) для \(x < -1\).
\(x = -1 — 2\)
\(x = -3\)
Значение \(x = -3\) удовлетворяет условию \(x < -1\).
Случай 2: \(x^2 = -1\) для \( -1 \le x \le 2 \).
Уравнение \(x^2 = -1\) не имеет действительных решений.
Случай 3: \(x+2 = -1\) для \(x > 2\).
\(x = -1 — 2\)
\(x = -3\)Значение \(x = -3\) не удовлетворяет условию \(x > 2\). Решений нет на этом участке.
Таким образом, при \(f(x) = -1\), значение аргумента: \(x = -3\).