ГДЗ по Алгебре 7 Класс Номер 46.29 Мордкович — Подробные Ответы

Постройте график функции: а) y= система x², если -2 ≤ x ≤ -1; x, если -1 < x ≤ 1; -x², если 1 < x ≤ 2; б) y= система 2x, если -4 ≤ x ≤ -1; -x², если -1 < x ≤ 0; -x², если 0 < x ≤ 3.

а)
\( \text{Определим функцию на первом интервале: } y = x^2 \text{ при } -2 \le x \le -1 \)
\( \text{Определим функцию на втором интервале: } y = x \text{ при } -1 < x \le 1 \)
\( \text{Определим функцию на третьем интервале: } y = -x^2 \text{ при } 1 < x \le 2 \)

Ответ: \( y = \begin{cases} x^2, & \text{если } -2 \le x \le -1 \\ x, & \text{если } -1 < x \le 1 \\ -x^2, & \text{если } 1 < x \le 2 \end{cases} \)

б)
\( \text{Определим функцию на первом интервале: } y = 2x \text{ при } -4 \le x \le -1 \)
\( \text{Определим функцию на втором интервале: } y = -x^2 \text{ при } -1 < x \le 0 \)
\( \text{Определим функцию на третьем интервале: } y = -x^2 \text{ при } 0 < x \le 3 \)
\( \text{Объединим второй и третий интервалы, так как функция одинакова и непрерывна в точке } x=0: \)
\( y = -x^2 \text{ при } -1 < x \le 3 \)

Ответ: \( y = \begin{cases} 2x, & \text{если } -4 \le x \le -1 \\ -x^2, & \text{если } -1 < x \le 3 \end{cases} \)

Условие: Постройте график функции:

а)
\(y=\begin{cases} x^2, & \text{если } -2 \le x \le -1 \\ x, & \text{если } -1 < x \le 1 \\ -x^2, & \text{если } 1 < x \le 2 \end{cases}\);

б)
\(y=\begin{cases} 2x, & \text{если } -4 \le x \le -1 \\ -x^2, & \text{если } -1 < x \le 0 \\ -x^2, & \text{если } 0 < x \le 3 \end{cases}\)

Решение:
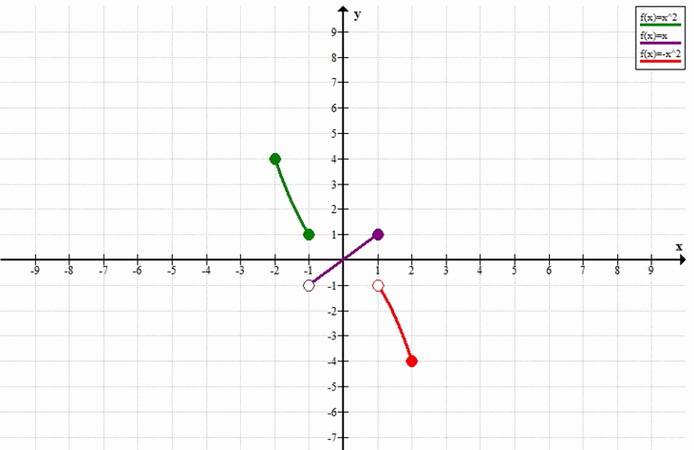
а) Построение графика функции \(y=\begin{cases} x^2, & \text{если } -2 \le x \le -1 \\ x, & \text{если } -1 < x \le 1 \\ -x^2, & \text{если } 1 < x \le 2 \end{cases}\)

1. Рассмотрим первый участок функции: \(y = x^2\) при \(-2 \le x \le -1\).
Это часть параболы, ветви которой направлены вверх.
Вычислим значения функции на концах интервала:
При \(x = -2\), \(y = (-2)^2 = 4\). Получаем точку \((-2, 4)\).
При \(x = -1\), \(y = (-1)^2 = 1\). Получаем точку \((-1, 1)\).
Этот участок графика представляет собой дугу параболы, соединяющую точки \((-2, 4)\) и \((-1, 1)\), включая обе конечные точки.

2. Рассмотрим второй участок функции: \(y = x\) при \(-1 < x \le 1\).
Это часть прямой линии.
Вычислим значения функции на концах интервала:
При \(x = -1\), \(y = -1\). Получаем точку \((-1, -1)\). Эта точка не включена в интервал, поэтому на графике она будет «выколотой».
При \(x = 1\), \(y = 1\). Получаем точку \((1, 1)\). Эта точка включена в интервал.
Этот участок графика представляет собой отрезок прямой, соединяющий точку \((-1, -1)\) (выколотая) и \((1, 1)\) (включенная).

3. Рассмотрим третий участок функции: \(y = -x^2\) при \(1 < x \le 2\).
Это часть параболы, ветви которой направлены вниз.
Вычислим значения функции на концах интервала:
При \(x = 1\), \(y = -(1)^2 = -1\). Получаем точку \((1, -1)\). Эта точка не включена в интервал, поэтому на графике она будет «выколотой».
При \(x = 2\), \(y = -(2)^2 = -4\). Получаем точку \((2, -4)\). Эта точка включена в интервал.
Этот участок графика представляет собой дугу параболы, соединяющую точки \((1, -1)\) (выколотая) и \((2, -4)\) (включенная).

4. График функции состоит из этих трех участков. Наблюдаются разрывы в точках \(x = -1\) и \(x = 1\).

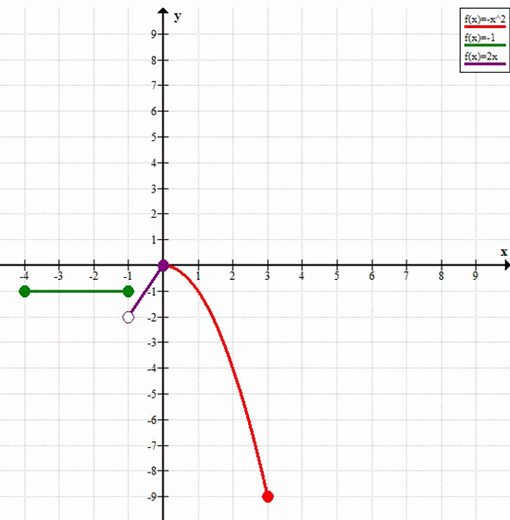
б) Построение графика функции \(y=\begin{cases} 2x, & \text{если } -4 \le x \le -1 \\ -x^2, & \text{если } -1 < x \le 0 \\ -x^2, & \text{если } 0 < x \le 3 \end{cases}\)

1. Заметим, что второй и третий участки функции описываются одной и той же формулой \(y = -x^2\).
Объединим эти участки в один: \(y = -x^2\) при \(-1 < x \le 3\).

2. Рассмотрим первый участок функции: \(y = 2x\) при \(-4 \le x \le -1\).
Это часть прямой линии.
Вычислим значения функции на концах интервала:
При \(x = -4\), \(y = 2(-4) = -8\). Получаем точку \((-4, -8)\).
При \(x = -1\), \(y = 2(-1) = -2\). Получаем точку \((-1, -2)\).
Этот участок графика представляет собой отрезок прямой, соединяющий точки \((-4, -8)\) и \((-1, -2)\), включая обе конечные точки.

3. Рассмотрим объединенный второй участок функции: \(y = -x^2\) при \(-1 < x \le 3\).
Это часть параболы, ветви которой направлены вниз.
Вычислим значения функции на концах интервала и в ключевой точке (вершине параболы):
При \(x = -1\), \(y = -(-1)^2 = -1\). Получаем точку \((-1, -1)\). Эта точка не включена в интервал, поэтому на графике она будет «выколотой».
При \(x = 0\), \(y = -(0)^2 = 0\). Получаем точку \((0, 0)\). Эта точка включена в интервал и является вершиной параболы.
При \(x = 3\), \(y = -(3)^2 = -9\). Получаем точку \((3, -9)\). Эта точка включена в интервал.
Этот участок графика представляет собой дугу параболы, соединяющую точки \((-1, -1)\) (выколотая) и \((3, -9)\) (включенная), проходящую через \((0, 0)\).

4. График функции состоит из этих двух участков. Наблюдается разрыв в точке \(x = -1\).

Ответ:
а) График функции состоит из трех участков:
1. Дуга параболы \(y = x^2\) от точки \((-2, 4)\) до точки \((-1, 1)\), включая обе точки.
2. Отрезок прямой \(y = x\) от точки \((-1, -1)\) (выколотая) до точки \((1, 1)\) (включенная).
3. Дуга параболы \(y = -x^2\) от точки \((1, -1)\) (выколотая) до точки \((2, -4)\), включая точку \((2, -4)\).
б) График функции состоит из двух участков:
1. Отрезок прямой \(y = 2x\) от точки \((-4, -8)\) до точки \((-1, -2)\), включая обе точки.
2. Дуга параболы \(y = -x^2\) от точки \((-1, -1)\) (выколотая) до точки \((3, -9)\), включая точку \((3, -9)\) и проходящая через \((0, 0)\).