ГДЗ по Алгебре 7 Класс Номер 46.30 Мордкович — Подробные Ответы

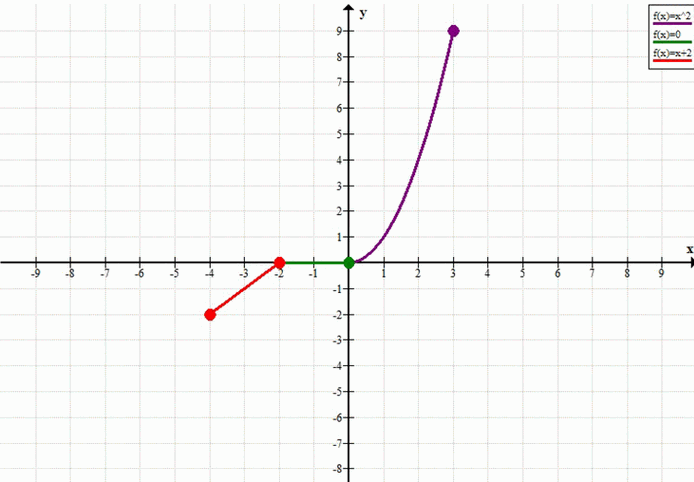
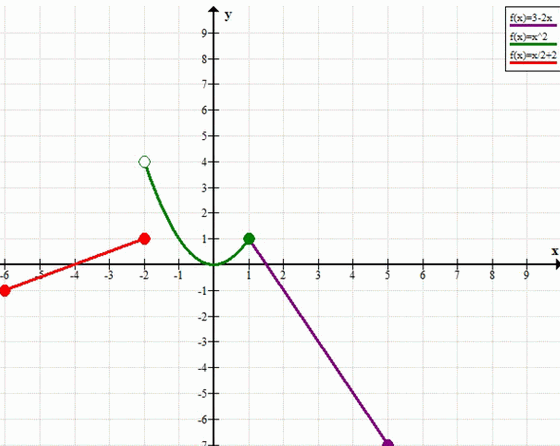
а) y= система x+2, если -4 ≤ x ≤ -2; 0, если -2 < x ≤ 0; x², если 0 < x ≤ 3; б) y= система x:2+2, если -6 ≤ x ≤ -2; -x², если -2 < x ≤ 1; 3-2x, если 1 < x ≤ 5. Используя заданный график функции, установите: 1) какова область определения функции \(у = f(x)\); 2) чему равны наименьшее и наибольшее значения функции; 3) является ли функция непрерывной; если нет, то в каких точках она претерпевает разрыв; 4) при каких значениях аргумента значение функции равно нулю, больше нуля, меньше нуля; 5) где функция возрастает, где убывает.

а) \(
y =
\begin{cases}
x + 2, & -4 \leq x \leq -2, \\
0, & -2 < x \leq 0, \\
x^2, & 0 < x \leq 3.
\end{cases}
\)

б) \(
y =
\begin{cases}
\frac{x}{2} + 2, & -6 \leq x \leq -2, \\
x^2, & -2 < x \leq 1, \\
3 — 2x, & 1 < x \leq 5.
\end{cases}
\)

а) Функция задана следующим образом:

\[
y =
\begin{cases}
x + 2, & -4 \leq x \leq -2, \\
0, & -2 < x \leq 0, \\
x^2, & 0 < x \leq 3.
\end{cases}
\]

Эта функция состоит из трёх частей, каждая из которых определена на своём промежутке.

Первая ветвь: \(y = x + 2\) при \(-4 \leq x \leq -2\).
Это линейная функция с угловым коэффициентом 1, то есть прямая, возрастает.
— При \(x = -4\): \(y = -4 + 2 = -2\),
— При \(x = -2\): \(y = -2 + 2 = 0\).
График — отрезок прямой от точки \((-4; -2)\) до точки \((-2; 0)\), включая оба конца (так как неравенства нестрогие).

Вторая ветвь: \(y = 0\) при \(-2 < x \leq 0\).
Это постоянная функция, график которой — горизонтальный отрезок на уровне \(y = 0\).
— Точка \(x = -2\) не входит (знак «<»), поэтому в \((-2; 0)\) стоит «выколотая» точка,
— Точка \(x = 0\) входит, значение \(y = 0\).
Таким образом, отрезок от \((-2; 0)\) (без точки) до \((0; 0)\) (с точкой).

Третья ветвь: \(y = x^2\) при \(0 < x \leq 3\).
Это часть параболы, ветви направлены вверх.
— При \(x \to 0^+\): \(y \to 0\), но \(x = 0\) не входит, поэтому начало — «выколотая» точка у начала координат,
— При \(x = 3\): \(y = 9\), точка \((3; 9)\) включена.
График — дуга параболы от начала координат (без точки) до \((3; 9)\).

Область определения всей функции: \([-4; 3]\).
Функция непрерывна везде, кроме, возможно, точки \(x = -2\), но поскольку слева предел равен 0 и справа значение тоже стремится к 0, а в самой точке \(x = -2\) функция определена как 0 (по первой ветви), то разрывов нет. В точке \(x = 0\) слева \(y = 0\), справа \(y \to 0\), но значение при \(x = 0\) задано второй ветвью как 0, поэтому функция непрерывна и там.

б) Функция задана следующим образом:

\[
y =
\begin{cases}
\frac{x}{2} + 2, & -6 \leq x \leq -2, \\
x^2, & -2 < x \leq 1, \\
3 — 2x, & 1 < x \leq 5.
\end{cases}
\]

Эта функция также состоит из трёх частей.

Первая ветвь: \(y = \frac{x}{2} + 2\) при \(-6 \leq x \leq -2\).
Это линейная убывающая функция (угловая коэффициент \(= \frac{1}{2} > 0\), но так как \(x\) отрицательный, значение уменьшается при движении вправо? Нет — на самом деле, коэффициент положительный, значит, функция возрастает).
— При \(x = -6\): \(y = \frac{-6}{2} + 2 = -3 + 2 = -1\),
— При \(x = -2\): \(y = \frac{-2}{2} + 2 = -1 + 2 = 1\).
График — отрезок прямой от \((-6; -1)\) до \((-2; 1)\), оба конца включены.

Вторая ветвь: \(y = x^2\) при \(-2 < x \leq 1\).
Это часть параболы.
— При \(x \to -2^+\): \(y \to 4\), но \(x = -2\) не входит,
— При \(x = 0\): \(y = 0\),
— При \(x = 1\): \(y = 1\), точка включена.
График — дуга параболы от точки, близкой к \((-2; 4)\) (без точки), через вершину \((0; 0)\), до \((1; 1)\).

Третья ветвь: \(y = 3 — 2x\) при \(1 < x \leq 5\).
Это линейная убывающая функция (коэффициент при \(x\) отрицательный).
— При \(x \to 1^+\): \(y \to 3 — 2 = 1\), но \(x = 1\) не входит,
— При \(x = 5\): \(y = 3 — 10 = -7\), точка включена.
График — отрезок прямой от точки, близкой к \((1; 1)\) (без точки), до \((5; -7)\).

Анализ непрерывности:
— В точке \(x = -2\):
— Слева (первая ветвь): \(y = 1\),
— Справа (вторая ветвь): \(y \to 4\).
→ Разрыв: значения не совпадают.
— В точке \(x = 1\):
— Слева (вторая ветвь): \(y = 1\),
— Справа (третья ветвь): \(y \to 1\).
→ Хотя обе стороны стремятся к 1, точка \(x = 1\) включена во вторую ветвь (\(y = 1\)), а третья ветвь начинается после неё. График будет иметь «стык» без разрыва по значению, но формально в \(x = 1\) функция определена, и предел справа совпадает, поэтому функция непрерывна в этой точке.

Область определения: \([-6; 5]\).