ГДЗ по Алгебре 7 Класс Номер 46.41 Мордкович — Подробные Ответы

Дана функция у = f(x), где f(x) = система -1, если -3 ≤ х ≤ -1; -x², если -1 < х ≤ 1; x, если 1 < x ≤ 6. а) Вычислите f(-2), f(4), f(-1), f(1), f(5); б) постройте график функции \(у = f(x)\); в) опишите свойства функции у = f(x) с помощью построенного графика

а) Вычислите f(-2), f(4), f(-1), f(1), f(5);

\( \text{Для } f(-2): \text{ так как } -3 \le -2 \le -1, \text{ используем правило } f(x) = -1. \)
\( f(-2) = -1 \)
Ответ: -1

\( \text{Для } f(4): \text{ так как } 1 < 4 \le 6, \text{ используем правило } f(x) = x. \)
\( f(4) = 4 \)
Ответ: 4

\( \text{Для } f(-1): \text{ так как } -3 \le -1 \le -1, \text{ используем правило } f(x) = -1. \)
\( f(-1) = -1 \)
Ответ: -1

\( \text{Для } f(1): \text{ так как } -1 < 1 \le 1, \text{ используем правило } f(x) = -x^2. \)
\( f(1) = -(1)^2 \)
\( f(1) = -1 \)
Ответ: -1

\( \text{Для } f(5): \text{ так как } 1 < 5 \le 6, \text{ используем правило } f(x) = x. \)
\( f(5) = 5 \)
Ответ: 5

б) постройте график функции \(у = f(x)\);

\( \text{График функции состоит из трех частей:} \)
\( \text{1. Отрезок прямой } y = -1 \text{ для } x \in [-3, -1]. \text{ Это горизонтальный отрезок, соединяющий точки } (-3, -1) \text{ и } (-1, -1). \)
\( \text{2. Часть параболы } y = -x^2 \text{ для } x \in (-1, 1]. \text{ Эта часть начинается в точке } (-1, -1) \text{ (включительно, так как функция непрерывна в } x=-1), \text{ проходит через вершину } (0, 0) \text{ и заканчивается в точке } (1, -1) \text{ (включительно).} \)
\( \text{3. Отрезок прямой } y = x \text{ для } x \in (1, 6]. \text{ Эта часть начинается в точке } (1, 1) \text{ (не включительно, открытый круг) и заканчивается в точке } (6, 6) \text{ (включительно, закрытый круг).} \)

Ответ: График описан выше.

в) опишите свойства функции \(у = f(x) с помощью построенного графика.\)
\( \text{Свойства функции } y = f(x): \)
\( \text{1. Область определения: } D(f) = [-3, 6]. \)
\( \text{2. Область значений: } E(f) = [-1, 0] \cup (1, 6]. \)
\( \text{3. Нули функции: } x = 0. \)
\( \text{4. Промежутки знакопостоянства:} \)
\( \text{ } f(x) < 0 \text{ при } x \in [-3, -1] \cup (-1, 0) \cup (0, 1]. \)
\( \text{ } f(x) > 0 \text{ при } x \in (1, 6]. \)
\( \text{5. Монотонность:} \)
\( \text{ Функция постоянна на } [-3, -1]. \)
\( \text{ Функция возрастает на } (-1, 0]. \)
\( \text{ Функция убывает на } (0, 1]. \)
\( \text{ Функция возрастает на } (1, 6]. \)
\( \text{6. Экстремумы:} \)
\( \text{ Локальный максимум: } f(0) = 0. \)
\( \text{ Глобальный максимум: } f(6) = 6. \)
\( \text{ Глобальный минимум: } f(x) = -1 \text{ на } [-3, -1] \text{ и } f(1) = -1. \)
\( \text{7. Непрерывность:} \)
\( \text{ Функция непрерывна на } [-3, 1]. \)
\( \text{ Функция непрерывна на } (1, 6]. \)
\( \text{ Функция имеет разрыв второго рода (скачок) в точке } x = 1. \)
\( \text{8. Четность/Нечетность: Функция не является ни четной, ни нечетной.} \)
Ответ: Свойства функции описаны выше.

Условие: Дана функция \(у = f(x)\), где
\(
f(x) =
\begin{cases}
-1, & \text{если } -3 \le x \le -1 \\
-x^2, & \text{если } -1 < x \le 1 \\
x, & \text{если } 1 < x \le 6
\end{cases}
\)
а) Вычислите \(f(-2)\), \(f(4)\), \(f(-1)\), \(f(1)\), \(f(5)\);
б) постройте график функции \(у = f(x)\);
в) опишите свойства функции \(у = f(x)\) с помощью построенного графика.

Решение:
а) Вычислим значения функции:
Для \(f(-2)\): \(x = -2\) находится в первом интервале \([-3, -1]\).
\(f(-2) = -1\)

Для \(f(4)\): \(x = 4\) находится в третьем интервале \((1, 6]\).
\(f(4) = 4\)

Для \(f(-1)\): \(x = -1\) находится в первом интервале \([-3, -1]\).
\(f(-1) = -1\)

Для \(f(1)\): \(x = 1\) находится во втором интервале \((-1, 1]\).
\(f(1) = -(1)^2 = -1\)

Для \(f(5)\): \(x = 5\) находится в третьем интервале \((1, 6]\).
\(f(5) = 5\)

б) Построим график функции \(у = f(x)\):
График состоит из трех частей:
1. Для \(x \in [-3, -1]\), \(y = -1\). Это горизонтальный отрезок от точки \( (-3, -1) \) до точки \( (-1, -1) \), включая обе конечные точки.
2. Для \(x \in (-1, 1]\), \(y = -x^2\). Это часть параболы, ветви которой направлены вниз.
При \(x \to -1^+\), \(y \to -(-1)^2 = -1\). Точка \( (-1, -1) \) не включается (выколотая точка).
При \(x = 0\), \(y = -(0)^2 = 0\). Точка \( (0, 0) \).
При \(x = 1\), \(y = -(1)^2 = -1\). Точка \( (1, -1) \) включается (закрашенная точка).
3. Для \(x \in (1, 6]\), \(y = x\). Это часть прямой линии.
При \(x \to 1^+\), \(y \to 1\). Точка \( (1, 1) \) не включается (выколотая точка).
При \(x = 6\), \(y = 6\). Точка \( (6, 6) \) включается (закрашенная точка).

в) Опишем свойства функции \(у = f(x)\) с помощью построенного графика:
1. Область определения: \(D(f) = [-3; 6]\).
2. Область значений: \(E(f) = [-1; 0] \cup (1; 6]\).
3. Нули функции: \(f(x) = 0\) при \(x = 0\).
4. Промежутки знакопостоянства:
\(f(x) < 0\) при \(x \in [-3; -1] \cup (-1; 0) \cup (0; 1]\).
\(f(x) > 0\) при \(x \in (1; 6]\).
5. Монотонность:
Функция постоянна на промежутке \( [-3; -1] \).
Функция возрастает на промежутке \( (-1; 0] \).
Функция убывает на промежутке \( [0; 1] \).
Функция возрастает на промежутке \( (1; 6] \).
6. Экстремумы:
Локальный максимум: \(f(0) = 0\).
Наибольшее значение функции: \(f(6) = 6\).
Наименьшее значение функции: \(f(x) = -1\) на промежутке \( [-3; -1] \) и в точке \( x=1 \).
7. Непрерывность: Функция непрерывна на промежутках \( [-3; -1] \), \( (-1; 1] \) и \( (1; 6] \). Функция имеет разрыв (скачок) в точке \( x = 1 \).

Ответ:
а)
\(f(-2) = -1\), \(f(4) = 4\), \(f(-1) = -1\), \(f(1) = -1\), \(f(5) = 5\).
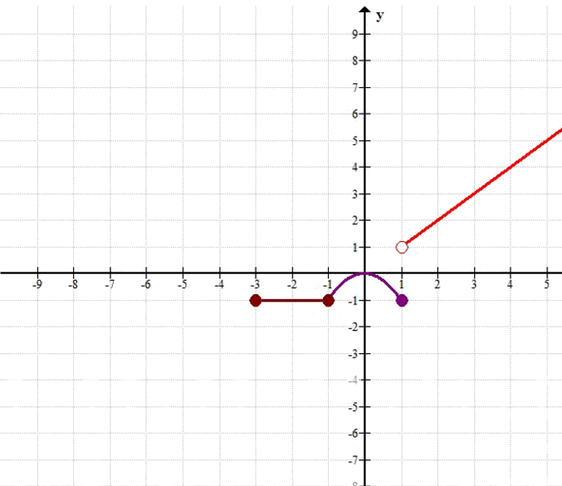
б) График функции состоит из трех частей: горизонтального отрезка \(y=-1\) на \([-3, -1]\), части параболы \(y=-x^2\) на \((-1, 1]\) и отрезка прямой \(y=x\) на \((1, 6]\).
в) Область определения \(D(f) = [-3; 6]\), область значений \(E(f) = [-1; 0] \cup (1; 6]\), нуль функции \(x=0\). Функция постоянна на \( [-3; -1] \), возрастает на \( (-1; 0] \) и \( (1; 6] \), убывает на \( [0; 1] \). Локальный максимум \(f(0)=0\). Наибольшее значение \(f(6)=6\), наименьшее значение \(f(x)=-1\) на \( [-3; -1] \) и в точке \( x=1 \). Функция имеет разрыв в точке \( x=1 \).