ГДЗ по Алгебре 7 Класс Номер 46.42 Мордкович — Подробные Ответы

Дана функция у = f(x), где f(x) = система 1, если -3 ≤ х ≤ -1; 2x+2, если -1 < х ≤ 2; x, если 2 < x < 4. а) Вычислите f(-3), f(2), f(0), f(-1), f(\(\frac{1}{2}\)); б) постройте график функции \(у = f(x)\); в) опишите свойства функции у = f(x) с помощью построенного графика.

а)
\( f(-3) = 1 \), \( f(2) = 6 \), \( f(0) = 2 \), \( f(-1) = 1 \), \( f\!\left(\frac{1}{2}\right) = 3 \).

б)
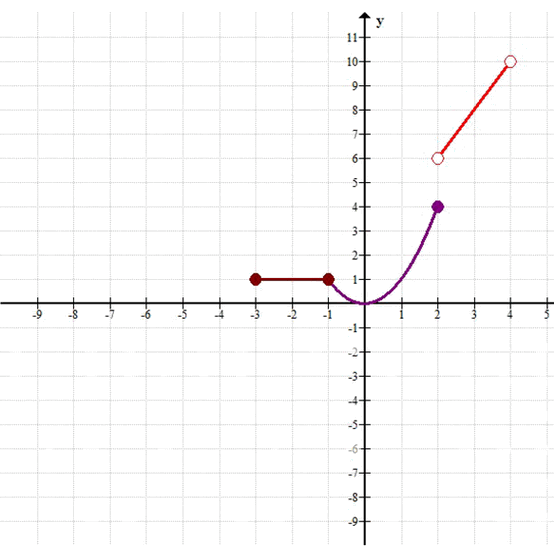
График состоит из трёх частей:
— отрезок \(y = 1\) на \([-3, -1]\) (обе точки включены);
— отрезок \(y = 2x + 2\) на \((-1, 2]\) (точка \((-1, 0)\) выколота, \((2, 6)\) — закрашена);
— отрезок \(y = x\) на \((2, 4)\) (обе точки выколоты).

в)
— Область определения: \([-3, 4)\)
— Область значений: \((0, 6]\)
— Нулей нет; \(f(x) > 0\) на всей области
— Постоянна на \([-3, -1]\), возрастает на \((-1, 2]\) и \((2, 4)\)
— Наибольшее значение: \(6\) (при \(x = 2\)); наименьшего значения нет
— Разрывы в точках \(x = -1\) и \(x = 2\)

а) Вычислите \( f(-3), f(2), f(0), f(-1), f\left(\frac{1}{2}\right) \)
\( f(-3) \):
Поскольку \( -3 \le -3 \le -1 \), используем правило \( f(x) = 1 \).
\( f(-3) = 1 \)
\( f(2) \):
Поскольку \( -1 < 2 \le 2 \), используем правило \( f(x) = 2x+2 \).
\( f(2) = 2(2) + 2 \)
\( f(2) = 4 + 2 \)
\( f(2) = 6 \)
\( f(0) \):
Поскольку \( -1 < 0 \le 2 \), используем правило \( f(x) = 2x+2 \).
\( f(0) = 2(0) + 2 \)
\( f(0) = 0 + 2 \)
\( f(0) = 2 \)
\( f(-1) \):
Поскольку \( -3 \le -1 \le -1 \), используем правило \( f(x) = 1 \).
\( f(-1) = 1 \)
\( f\left(\frac{1}{2}\right) \):
Поскольку \( -1 < \frac{1}{2} \le 2 \), используем правило \( f(x) = 2x+2 \).
\( f\left(\frac{1}{2}\right) = 2\left(\frac{1}{2}\right) + 2 \)
\( f\left(\frac{1}{2}\right) = 1 + 2 \)
\( f\left(\frac{1}{2}\right) = 3 \)

Ответ: \( f(-3)=1, f(2)=6, f(0)=2, f(-1)=1, f\left(\frac{1}{2}\right)=3 \)

б) Постройте график функции \( у = f(x) \)

График функции \( у = f(x) \) состоит из трех частей:
1. Для \( x \in [-3, -1] \):
\( y = 1 \)
Это горизонтальный отрезок прямой, соединяющий точки \( (-3, 1) \) и \( (-1, 1) \). Обе точки включены.
2. Для \( x \in (-1, 2] \):
\( y = 2x+2 \)
Это отрезок прямой. Начальная точка \( (-1, 2(-1)+2) = (-1, 0) \) является выколотой. Конечная точка \( (2, 2(2)+2) = (2, 6) \) является закрашенной.
3. Для \( x \in (2, 4) \):
\( y = x \)
Это отрезок прямой. Начальная точка \( (2, 2) \) является выколотой. Конечная точка \( (4, 4) \) является выколотой.

Ответ: График состоит из отрезка \( y=1 \) для \( x \in [-3, -1] \), отрезка \( y=2x+2 \) для \( x \in (-1, 2] \) (с выколотой точкой \( (-1,0) \) и закрашенной точкой \( (2,6) \)), и отрезка \( y=x \) для \( x \in (2, 4) \) (с выколотыми точками \( (2,2) \) и \( (4,4) \)).

в) Опишите свойства функции \( у = f(x) \) с помощью построенного графика.

1. Область определения:
\( D(f) = [-3, 4) \)
2. Область значений:
\( E(f) = (0, 6] \)
3. Нули функции:
Функция не имеет нулей, так как \( f(x) > 0 \) на всей области определения.
4. Знакопостоянство:
\( f(x) > 0 \) для всех \( x \in [-3, 4) \).
5. Монотонность:
Функция постоянна на интервале \( [-3, -1] \).
Функция возрастает на интервале \( (-1, 2] \).
Функция возрастает на интервале \( (2, 4) \).
В целом, функция является неубывающей на своей области определения.
6. Экстремумы:
Наибольшее значение функции: \( y_{max} = f(2) = 6 \).
Наименьшего значения функция не имеет (инфимум равен 0).
7. Непрерывность:
Функция имеет разрывы первого рода (скачки) в точках \( x = -1 \) и \( x = 2 \).

Ответ: \( D(f) = [-3, 4) \), \( E(f) = (0, 6] \), нулей нет, \( f(x) > 0 \) на \( [-3, 4) \), постоянна на \( [-3, -1] \), возрастает на \( (-1, 2] \) и \( (2, 4) \), \( y_{max} = 6 \), наименьшего значения нет, разрывы в \( x = -1 \) и \( x = 2 \).