ГДЗ по Алгебре 7 Класс Номер 46.43 Мордкович — Подробные Ответы

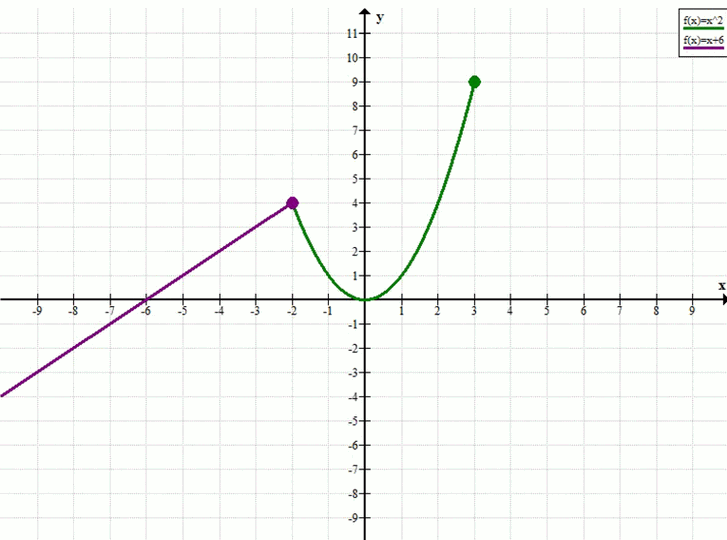
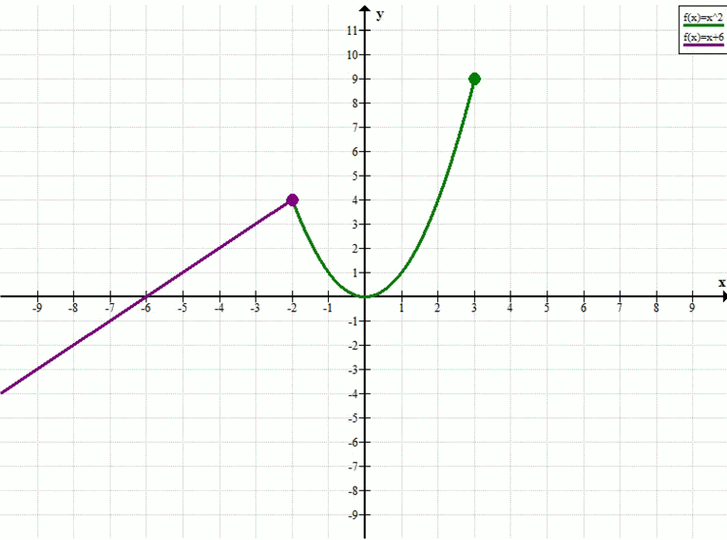
При каких значениях b уравнение f(x) = b, где f(x) = система х + 6, если х ≤ -2; x², если -2 < х ≤ 3, а) имеет один корень; б) имеет два корня; в) имеет три корня; г) не имеет корней?

а) имеет один корень
\( b < 0 \)
\( 4 < b \le 9 \)
Ответ: \( (-\infty, 0) \cup (4, 9] \)

б) имеет два корня
\( b = 0 \)
\( b = 4 \)
Ответ: \( \{0, 4\} \)

в) имеет три корня
\( 0 < b < 4 \)
Ответ: \( (0, 4) \)

г) не имеет корней
\( b > 9 \)
Ответ: \( (9, +\infty) \)

Задана кусочная функция:

\[
f(x) =
\begin{cases}
x + 6, & x \leq -2 \\
x^2, & -2 < x \leq 3
\end{cases}
\]

Эта функция состоит из двух частей:
— при \(x \leq -2\) — линейная функция \(y = x + 6\),
— при \(-2 < x \leq 3\) — параболическая часть \(y = x^2\).

Область определения: \((-\infty; 3]\).

График функции имеет «излом» в точке \(x = -2\), где происходит переход от прямой к параболе.
В точке \(x = -2\) значение функции вычисляется по первой формуле:
\(f(-2) = -2 + 6 = 4\).
При подходе справа: \(\lim_{x \to -2^+} x^2 = 4\), поэтому функция **непрерывна** в этой точке.

На промежутке \((-\infty; -2]\) функция возрастает (угловая коэффициент равен 1), на \((-2; 3]\) — также возрастает (парабола \(y = x^2\) возрастает при \(x > 0\), но на интервале \((-2; 0]\) она убывает).
Таким образом, общее поведение:
— на \((-\infty; -2]\): возрастает от \(-\infty\) до 4,
— на \([-2; 0]\): убывает от 4 до 0,
— на \([0; 3]\): возрастает от 0 до 9.

Наибольшее значение: \(f(3) = 9\), наименьшее значение: не существует (функция не ограничена снизу слева), но на области \([-2; 3]\) минимум равен 0 (при \(x = 0\)).

Анализ количества корней уравнения \(f(x) = b\) в зависимости от параметра \(b\)

Рассмотрим, сколько решений имеет уравнение \(f(x) = b\) при различных значениях параметра \(b\).

а) Один корень — при \(b < 0\) и \(b \in (4; 9]\)

— При \(b < 0\):
Уравнение \(f(x) = b\) может иметь решение только на левой ветви, так как правая часть \(x^2 \geq 0\).
Решаем \(x + 6 = b \Rightarrow x = b — 6\).
Это решение принадлежит области \(x \leq -2\), если \(b — 6 \leq -2 \Rightarrow b \leq 4\).
Так как \(b < 0\), условие выполняется, и корень единственный.

— При \(b \in (4; 9]\):
На левой ветви: \(x + 6 = b \Rightarrow x = b — 6\).
Но \(b > 4 \Rightarrow x > -2\), что выходит за область определения левой ветви — значит, корень здесь невозможен.
На правой ветви: \(x^2 = b \Rightarrow x = \pm\sqrt{b}\).
Однако \(x\) должен быть в интервале \((-2; 3]\).
Положительный корень \(x = \sqrt{b}\) всегда входит в \((0; 3]\), так как \(b \leq 9 \Rightarrow \sqrt{b} \leq 3\).
Отрицательный корень \(x = -\sqrt{b}\) должен быть больше \(-2\), то есть \(-\sqrt{b} > -2 \Rightarrow \sqrt{b} < 2 \Rightarrow b < 4\).
Но у нас \(b > 4\), поэтому отрицательный корень не входит в область.
Следовательно, только один корень: \(x = \sqrt{b}\).

б) Два корня — при \(b = 4\) и \(b = 0\)

— При \(b = 4\):
Левая ветвь: \(x + 6 = 4 \Rightarrow x = -2\) — входит в область.
Правая ветвь: \(x^2 = 4 \Rightarrow x = \pm 2\).
\(x = 2\) входит в область \((-2; 3]\), \(x = -2\) не входит (так как \(x > -2\) для второй ветви).
Таким образом, два корня: \(x = -2\) и \(x = 2\).

— При \(b = 0\):
Левая ветвь: \(x + 6 = 0 \Rightarrow x = -6\) — входит в область.
Правая ветвь: \(x^2 = 0 \Rightarrow x = 0\) — входит в область.
Два корня: \(x = -6\) и \(x = 0\).

в) Три корня — при \(b \in (0; 4)\)

— При \(b \in (0; 4)\):
Левая ветвь: \(x + 6 = b \Rightarrow x = b — 6\).
Так как \(b < 4\), то \(x < -2\) — корень существует.
Правая ветвь: \(x^2 = b \Rightarrow x = \pm\sqrt{b}\).
Оба корня входят в область:
— \(x = \sqrt{b} \in (0; 2) \subset (-2; 3]\),
— \(x = -\sqrt{b} \in (-2; 0) \subset (-2; 3]\), так как \(\sqrt{b} < 2\).
Итого три корня: \(x = b — 6\), \(x = -\sqrt{b}\), \(x = \sqrt{b}\).

г) Корней нет — при \(b > 9\)

— При \(b > 9\):
Левая ветвь: \(x + 6 = b \Rightarrow x = b — 6 > 3\), что выходит за область определения.
Правая ветвь: \(x^2 = b \Rightarrow x = \pm\sqrt{b}\).
Но \(\sqrt{b} > 3\), поэтому положительный корень не входит в область, а отрицательный \(-\sqrt{b} < -3 < -2\) — тоже не входит.
Следовательно, корней нет.