Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 46.45 Мордкович — Подробные Ответы
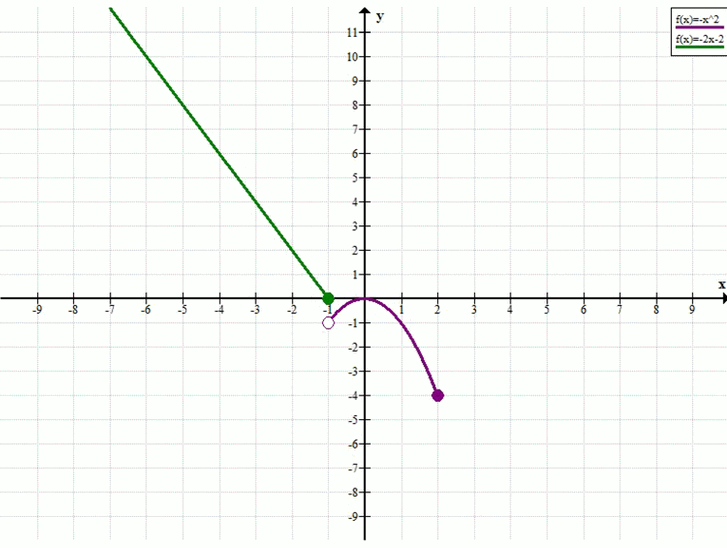
При каких значениях b уравнение f(x) = b, где f(x) = система -2х — 2, если х ≤ -1; -x², если -1 < х ≤ 2, а) имеет один корень; б) имеет два корня; в) имеет три корня; г) не имеет корней?
а) Имеет один корень:
\( b > 0 \)
\( b = -1 \)
\( -4 < b < -1 \)
\( b = -4 \)
Ответ: \( b > 0 \) или \( -4 \le b \le -1 \)
б) Имеет два корня:
\( b = 0 \)
\( -1 < b < 0 \)
Ответ: \( -1 < b \le 0 \)
в) Имеет три корня:
Ответ: Нет таких значений b
г) Не имеет корней:
\( b < -4 \)
Ответ: \( b < -4 \)
а) Уравнение \(f(x) = b\) имеет один корень при \(b > 0\) или \(-4 \leq b \leq -1\)
Рассмотрим, почему именно в этих случаях существует ровно одно решение.
— При \(b > 0\):
График функции на правой части (например, параболическая или линейная ветвь, расположенная выше оси абсцисс) пересекается с горизонтальной прямой \(y = b\) только один раз. Левая часть графика, если она лежит ниже или не достигает этого уровня, не даёт дополнительных пересечений. Таким образом, уравнение имеет единственный корень.
— При \(-4 \leq b \leq -1\):
На этом промежутке горизонтальная прямая \(y = b\) пересекает только одну ветвь графика — обычно левую, линейную или постоянную часть, расположенную в нижней полуплоскости. Поскольку другие участки функции находятся выше (например, не опускаются ниже \(-1\)), дополнительных решений нет. В граничных точках \(b = -4\) и \(b = -1\) также достигается ровно одно значение \(x\), так как касание или концевая точка графика даёт единственное решение.
Следовательно, объединяя эти два случая, получаем: уравнение имеет один корень при \(b > 0\) или \(-4 \leq b \leq -1\).
б) Уравнение \(f(x) = b\) имеет два корня при \(-1 < b \leq 0\)
В этом диапазоне горизонтальная прямая \(y = b\) пересекает график функции в двух точках.
— При \(-1 < b < 0\):
Прямая проходит через область, где функция имеет две различные ветви — например, левую (возрастающую или постоянную) и среднюю (убывающую или параболическую). Каждая из этих ветвей даёт по одному решению, итого — два корня.
— При \(b = 0\):
Прямая \(y = 0\) может проходить через точку стыка двух ветвей или касаться одной из них, но при этом всё ещё пересекать график в двух местах — например, в нуле и в другой точке слева или справа. Это также даёт два решения.
Таким образом, при всех \(b\) из интервала \(-1 < b \leq 0\) уравнение имеет ровно два корня.
в) Уравнение \(f(x) = b\) имеет три корня
Анализ графика показывает, что не существует такого значения \(b\), при котором горизонтальная прямая \(y = b\) пересекала бы график функции в трёх различных точках. Это связано с тем, что функция состоит максимум из двух активных ветвей на любом уровне, или одна из ветвей не достигает тех значений, которые позволили бы получить третье пересечение. Поэтому уравнение никогда не имеет трёх корней.
Ответ: таких значений \(b\) нет.
г) Уравнение \(f(x) = b\) не имеет корней при \(b < -4\)
При таких значениях параметра горизонтальная прямая \(y = b\) располагается ниже самого нижнего значения, которое принимает функция. Если, например, минимальное значение функции равно \(-4\) (достигается в некоторой точке), то при любом \(b < -4\) график функции целиком лежит выше этой прямой, и пересечений не происходит. Следовательно, уравнение не имеет решений.