ГДЗ по Алгебре 7 Класс Номер 46.46 Мордкович — Подробные Ответы

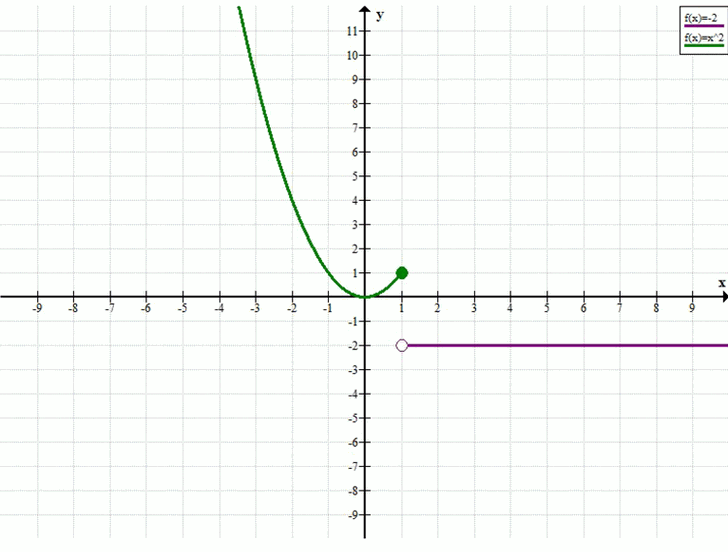
При каких значениях b уравнение f(x) = b, где f(x) = система x², если х ≤ 1; -2, если x > 1, а) имеет один корень; б) имеет два корня; в) имеет бесконечное множество корней; г) не имеет корней?

а) Один корень — при \( b = 0 \) или \( b > 1 \).
б) Два корня — при \( 0 < b \leq 1 \).
в) Бесконечно много корней — при \( b = -2 \).
г) Нет корней — при \( b < -2 \) или \( -2 < b < 0 \).

Условие: При каких значениях \( b \) уравнение \( f(x) = b \), где \( f(x) = \begin{cases} x^2, & \text{если } x \le 1 \\ -2, & \text{если } x > 1 \end{cases} \),

а) имеет один корень;

б) имеет два корня;

в) имеет бесконечное множество корней;

г) не имеет корней?

Решение:
Рассмотрим функцию \( f(x) \) и ее поведение на различных интервалах.
Функция \( f(x) \) определена как:
\( f(x) = x^2 \) при \( x \le 1 \)
\( f(x) = -2 \) при \( x > 1 \)

Проанализируем количество корней уравнения \( f(x) = b \) в зависимости от значения \( b \).

Случай 1: \( b < -2 \)
Если \( b < -2 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Поскольку \( x^2 \ge 0 \) для всех \( x \), уравнение \( x^2 = b \) не имеет решений, так как \( b < 0 \).
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = b \) не имеет решений, так как \( b \ne -2 \).
В этом случае уравнение не имеет корней.

Случай 2: \( b = -2 \)
Если \( b = -2 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = -2 \) не имеет решений, так как \( x^2 \ge 0 \).
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = -2 \) верно для всех \( x > 1 \). Это означает бесконечное множество корней.
В этом случае уравнение имеет бесконечное множество корней.

Случай 3: \( -2 < b < 0 \)
Если \( -2 < b < 0 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = b \) не имеет решений, так как \( b < 0 \).
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = b \) не имеет решений, так как \( b \ne -2 \).
В этом случае уравнение не имеет корней.

Случай 4: \( b = 0 \)
Если \( b = 0 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = 0 \) имеет одно решение \( x = 0 \). Поскольку \( 0 \le 1 \), это является корнем.
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = 0 \) не имеет решений.
В этом случае уравнение имеет один корень.

Случай 5: \( 0 < b < 1 \)
Если \( 0 < b < 1 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = b \) имеет два решения \( x = \sqrt{b} \) и \( x = -\sqrt{b} \).
Поскольку \( 0 < b < 1 \), то \( 0 < \sqrt{b} < 1 \). Оба решения \( \sqrt{b} \) и \( -\sqrt{b} \) удовлетворяют условию \( x \le 1 \).
Это дает два корня.
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = b \) не имеет решений, так как \( b > 0 \).
В этом случае уравнение имеет два корня.

Случай 6: \( b = 1 \)
Если \( b = 1 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = 1 \) имеет два решения \( x = 1 \) и \( x = -1 \).
Оба решения \( 1 \) и \( -1 \) удовлетворяют условию \( x \le 1 \).
Это дает два корня.
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = 1 \) не имеет решений.
В этом случае уравнение имеет два корня.

Случай 7: \( b > 1 \)
Если \( b > 1 \), то:
Для \( x \le 1 \), \( f(x) = x^2 \). Уравнение \( x^2 = b \) имеет два решения \( x = \sqrt{b} \) и \( x = -\sqrt{b} \).
Поскольку \( b > 1 \), то \( \sqrt{b} > 1 \). Решение \( x = \sqrt{b} \) не удовлетворяет условию \( x \le 1 \).
Решение \( x = -\sqrt{b} \) удовлетворяет условию \( x \le 1 \) (так как \( -\sqrt{b} < -1 \)).
Это дает один корень.
Для \( x > 1 \), \( f(x) = -2 \). Уравнение \( -2 = b \) не имеет решений, так как \( b > 1 \).
В этом случае уравнение имеет один корень.

Обобщим результаты:
а) Уравнение имеет один корень при \( b = 0 \) или \( b > 1 \).
б) Уравнение имеет два корня при \( 0 < b < 1 \) или \( b = 1 \).
в) Уравнение имеет бесконечное множество корней при \( b = -2 \).
г) Уравнение не имеет корней при \( b < -2 \) или \( -2 < b < 0 \).