ГДЗ по Алгебре 7 Класс Номер 46.47 Мордкович — Подробные Ответы

Решите графически уравнение: а) f(x) =1; б) f(x)=4; в) f(x)=9; г)f(x)=0, если f(x) = система 0,5x+5, если -10 ≤ x ≤ -2; x², если -2 < x ≤ 3.

а)
\( f(x) = 1 \)
Рассмотрим первый интервал: \( -10 \le x \le -2 \)
\( 0.5x + 5 = 1 \)
\( 0.5x = 1 — 5 \)
\( 0.5x = -4 \)
\( x = \frac{-4}{0.5} \)
\( x = -8 \)
Поскольку \( -10 \le -8 \le -2 \), \( x = -8 \) является решением.

Рассмотрим второй интервал: \( -2 < x \le 3 \)
\( x^2 = 1 \)
\( x = \pm \sqrt{1} \)
\( x = 1 \) или \( x = -1 \)
Поскольку \( -2 < 1 \le 3 \), \( x = 1 \) является решением.
Поскольку \( -2 < -1 \le 3 \), \( x = -1 \) является решением.

Ответ: -8; -1; 1

б)
\( f(x) = 4 \)
Рассмотрим первый интервал: \( -10 \le x \le -2 \)
\( 0.5x + 5 = 4 \)
\( 0.5x = 4 — 5 \)
\( 0.5x = -1 \)
\( x = \frac{-1}{0.5} \)
\( x = -2 \)
Поскольку \( -10 \le -2 \le -2 \), \( x = -2 \) является решением.

Рассмотрим второй интервал: \( -2 < x \le 3 \)
\( x^2 = 4 \)
\( x = \pm \sqrt{4} \)
\( x = 2 \) или \( x = -2 \)
Поскольку \( -2 < 2 \le 3 \), \( x = 2 \) является решением.
Поскольку \( x = -2 \) не принадлежит интервалу \( -2 < x \le 3 \), \( x = -2 \) не является решением для этого интервала.

Ответ: -2; 2

в)
\( f(x) = 9 \)
Рассмотрим первый интервал: \( -10 \le x \le -2 \)
\( 0.5x + 5 = 9 \)
\( 0.5x = 9 — 5 \)
\( 0.5x = 4 \)
\( x = \frac{4}{0.5} \)
\( x = 8 \)
Поскольку \( x = 8 \) не принадлежит интервалу \( -10 \le x \le -2 \), \( x = 8 \) не является решением.

Рассмотрим второй интервал: \( -2 < x \le 3 \)
\( x^2 = 9 \)
\( x = \pm \sqrt{9} \)
\( x = 3 \) или \( x = -3 \)
Поскольку \( -2 < 3 \le 3 \), \( x = 3 \) является решением.
Поскольку \( x = -3 \) не принадлежит интервалу \( -2 < x \le 3 \), \( x = -3 \) не является решением.

Ответ: 3

г)
\( f(x) = 0 \)
Рассмотрим первый интервал: \( -10 \le x \le -2 \)
\( 0.5x + 5 = 0 \)
\( 0.5x = -5 \)
\( x = \frac{-5}{0.5} \)
\( x = -10 \)
Поскольку \( -10 \le -10 \le -2 \), \( x = -10 \) является решением.

Рассмотрим второй интервал: \( -2 < x \le 3 \)
\( x^2 = 0 \)
\( x = 0 \)
Поскольку \( -2 < 0 \le 3 \), \( x = 0 \) является решением.

Ответ: -10; 0

Условие: Решите графически уравнение:

а)
\( f(x) = 1 \);

б)
\( f(x) = 4 \);

в)
\( f(x) = 9 \);

г)
\( f(x) = 0 \), если \( f(x) = \begin{cases} 0.5x + 5, & \text{если } -10 \le x \le -2 \\ x^2, & \text{если } -2 < x \le 3 \end{cases} \)

Решение:
Для графического решения построим график функции \( y = f(x) \) и прямые \( y = C \) для каждого случая, а затем найдем абсциссы точек их пересечения.

Построение графика функции \( y = f(x) \):
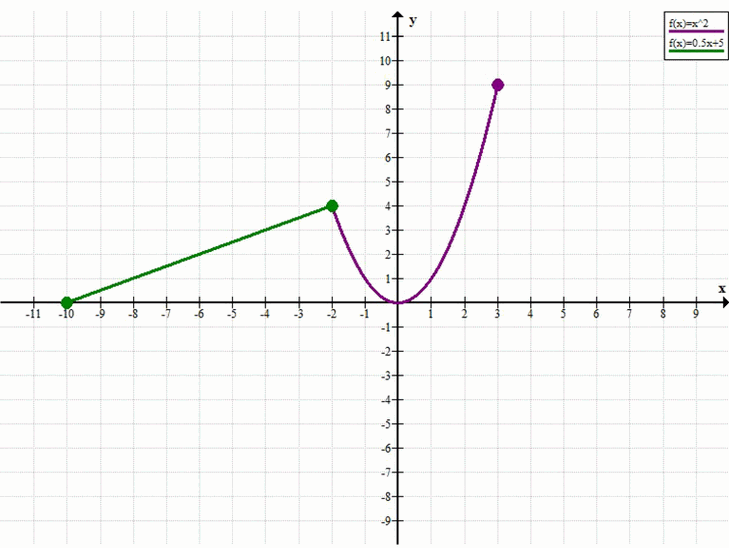
График состоит из двух частей:
1. Прямая \( y = 0.5x + 5 \) на отрезке \( [-10, -2] \).
При \( x = -10 \), \( y = 0.5(-10) + 5 = -5 + 5 = 0 \). Получаем точку \( (-10, 0) \).
При \( x = -2 \), \( y = 0.5(-2) + 5 = -1 + 5 = 4 \). Получаем точку \( (-2, 4) \).
Эта часть графика представляет собой отрезок, соединяющий точки \( (-10, 0) \) и \( (-2, 4) \).

2. Парабола \( y = x^2 \) на интервале \( (-2, 3] \).
При \( x = -2 \) (не включительно), \( y = (-2)^2 = 4 \). Это открытая точка \( (-2, 4) \).
При \( x = 0 \), \( y = 0^2 = 0 \). Получаем точку \( (0, 0) \).
При \( x = 3 \), \( y = 3^2 = 9 \). Получаем точку \( (3, 9) \).
Эта часть графика представляет собой часть параболы, проходящую через \( (0, 0) \) и \( (3, 9) \), начинающуюся «после» \( x = -2 \).

Теперь решим каждое уравнение графически, находя точки пересечения графика \( y = f(x) \) с соответствующей горизонтальной прямой \( y = C \).

а)
\( f(x) = 1 \)
Проводим горизонтальную прямую \( y = 1 \).
Ищем точки пересечения с графиком \( y = f(x) \).
1. Для первой части функции: \( 0.5x + 5 = 1 \)
\( 0.5x = 1 — 5 \)
\( 0.5x = -4 \)
\( x = -4 / 0.5 \)
\( x = -8 \)
Значение \( x = -8 \) находится в интервале \( [-10, -2] \). Это одно из решений.
2. Для второй части функции: \( x^2 = 1 \)
\( x = \pm \sqrt{1} \)
\( x = 1 \) или \( x = -1 \)
Оба значения \( x = 1 \) и \( x = -1 \) находятся в интервале \( (-2, 3] \). Это еще два решения.
Решения для

а): \( x = -8, x = -1, x = 1 \).

б)
\( f(x) = 4 \)
Проводим горизонтальную прямую \( y = 4 \).
Ищем точки пересечения с графиком \( y = f(x) \).
1. Для первой части функции: \( 0.5x + 5 = 4 \)
\( 0.5x = 4 — 5 \)
\( 0.5x = -1 \)
\( x = -1 / 0.5 \)
\( x = -2 \)
Значение \( x = -2 \) находится в интервале \( [-10, -2] \). Это одно из решений.
2. Для второй части функции: \( x^2 = 4 \)
\( x = \pm \sqrt{4} \)
\( x = 2 \) или \( x = -2 \)
Значение \( x = 2 \) находится в интервале \( (-2, 3] \). Это еще одно решение.
Значение \( x = -2 \) не входит в интервал \( (-2, 3] \).
Решения для

б): \( x = -2, x = 2 \).

в)
\( f(x) = 9 \)
Проводим горизонтальную прямую \( y = 9 \).
Ищем точки пересечения с графиком \( y = f(x) \).
1. Для первой части функции: \( 0.5x + 5 = 9 \)
\( 0.5x = 9 — 5 \)
\( 0.5x = 4 \)
\( x = 4 : 0.5 \)
\( x = 8 \)
Значение \( x = 8 \) не находится в интервале \( [-10, -2] \). Решений нет.
2. Для второй части функции: \( x^2 = 9 \)
\( x = \pm \sqrt{9} \)
\( x = 3 \) или \( x = -3 \)
Значение \( x = 3 \) находится в интервале \( (-2, 3] \). Это одно из решений.
Значение \( x = -3 \) не находится в интервале \( (-2, 3] \). Решений нет.
Решение для

в): \( x = 3 \).

г)
\( f(x) = 0 \)
Проводим горизонтальную прямую \( y = 0 \).
Ищем точки пересечения с графиком \( y = f(x) \).
1. Для первой части функции: \( 0.5x + 5 = 0 \)
\( 0.5x = -5 \)
\( x = -5 / 0.5 \)
\( x = -10 \)
Значение \( x = -10 \) находится в интервале \( [-10, -2] \). Это одно из решений.
2. Для второй части функции: \( x^2 = 0 \)
\( x = 0 \)
Значение \( x = 0 \) находится в интервале \( (-2, 3] \). Это еще одно решение.
Решения для г): \( x = -10, x = 0 \).

Ответы:

а)
\( x = -8, x = -1, x = 1 \);

б)
\( x = -2, x = 2 \);

в)
\( x = 3 \);

г)
\( x = -10, x = 0 \)