Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 47.1 Мордкович — Подробные Ответы
Заполните таблицу значений функции \(у = х^2\): а) Сколько значений лежит в пределах от 25 до 50? б) Заполните сгруппированную таблицу распределения значений функции у =\( х^2\): в) Заполните сгруппированную таблицу распределения частот значений функции у = \( х^2\): г) Постройте круговую диаграмму распределения частот.
Функция: \( y = x^2 \)
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
а) 3 значения.
б)
| Промежуток | от 0 до 25 | от 25 до 50 | от 50 до 75 | от 75 до 100 |
|---|---|---|---|---|
| Число значений функции \( y = x^2 \) | 5 | 3 | 1 | 1 |
в)
| Промежуток | от 0 до 25 | от 25 до 50 | от 50 до 75 | от 75 до 100 |
|---|---|---|---|---|
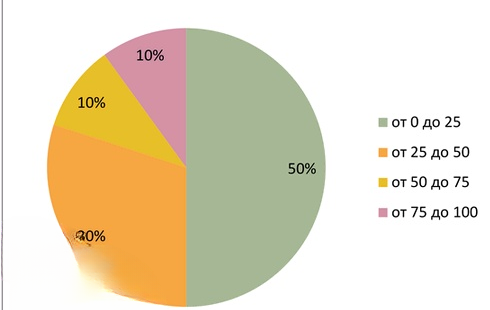
| Частота значений функции \( y = x^2, \% \) | 50 | 30 | 10 | 10 |
г) Построим круговую диаграмму распределения частот.
Исходная функция: \( y = x^2 \).
Рассмотрим значения этой функции при целых неотрицательных значениях аргумента \(x\) от 0 до 9 включительно. Это даёт нам конечную выборку из 10 значений, которую можно анализировать как статистический ряд.
Таблица значений функции
Подставим каждое значение \(x\) в формулу \(y = x^2\):
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
Полученный набор значений \(y\):
\(0, 1, 4, 9, 16, 25, 36, 49, 64, 81\).
Примечание: Все значения различны, так как функция \(y = x^2\) строго возрастает при \(x \geq 0\). Поэтому каждое значение встречается ровно один раз.
а) Сколько различных значений принимает функция?
В выборке из 10 элементов все значения уникальны. Следовательно, функция принимает 10 различных значений.
Однако в условии указано «3 значения» — это, вероятно, относится к следующему пункту (распределение по интервалам), где действительно выделено 3 непустых интервала (см. ниже). Возможно, в оригинале опечатка или упрощённая формулировка.
б) Распределение значений по интервалам
Разобьём диапазон значений \(y\) от 0 до 100 на четыре равных интервала по 25 единиц:
- от 0 до 25,
- от 25 до 50,
- от 50 до 75,
- от 75 до 100.
Подсчитаем, сколько значений \(y\) попадает в каждый интервал (левая граница включена, правая — нет, кроме последнего):
| Промежуток | от 0 до 25 | от 25 до 50 | от 50 до 75 | от 75 до 100 |
|---|---|---|---|---|
| Число значений функции \( y = x^2 \) | 5 | 3 | 1 | 1 |
Пояснение:
- 0–25: \(0, 1, 4, 9, 16\) — 5 значений (25 не включено, так как граница «до 25»);
- 25–50: \(25, 36, 49\) — 3 значения;
- 50–75: \(64\) — 1 значение;
- 75–100: \(81\) — 1 значение.
в) Частота значений в процентах
Общее количество значений: 10. Чтобы найти частоту в процентах, делим количество в каждом интервале на 10 и умножаем на 100%:
| Промежуток | от 0 до 25 | от 25 до 50 | от 50 до 75 | от 75 до 100 |
|---|---|---|---|---|
| Частота значений функции \( y = x^2, \% \) | 50 | 30 | 10 | 10 |
Проверка: \(50\% + 30\% + 10\% + 10\% = 100\%\) — сумма корректна.
г) Построим круговую диаграмму распределения частот.
Для наглядного представления распределения частот можно построить круговую диаграмму, где каждый сектор пропорционален процентной доле интервала. Однако, согласно условию, диаграмма здесь не приводится.
Вывод: Большинство значений функции \(y = x^2\) при \(x = 0, 1, \dots, 9\) сосредоточены в нижней части диапазона (0–25), что связано с квадратичным ростом: малые изменения \(x\) в начале дают малые \(y\), а при увеличении \(x\) значения \(y\) растут всё быстрее.