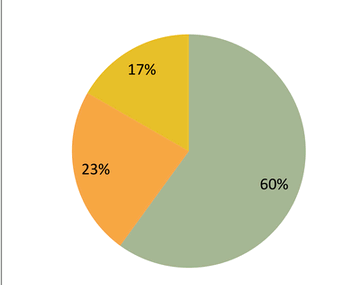Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 47.3 Мордкович — Подробные Ответы
а) Заполните таблицу распределения значений функции у = x², х = 0,1,2,28,29. б) Переведите эту таблицу в таблицу распределения процентных частот. в) Постройте круговую диаграмму распределения процентных частот. г) Разбейте промежуток от 0 до 1000 на три промежутка так, чтобы каждому из них принадлежало по 10 значений этой функции.
а)
| Промежуток | от 0 до 300 | от 300 до 600 | от 600 до 1000 |
|---|---|---|---|
| Число значений функции \( y = x^2 \) | 18 | 7 | 5 |
б)
| Промежуток | от 0 до 300 | от 300 до 600 | от 600 до 1000 |
|---|---|---|---|
| Частота значений функции \( y = x^2, \% \) | 60 | 23,3 | 16,7 |
г)
Например: от 0 до 99; от 99 до 399; от 399 до 1000.
Условие:
а) Заполните таблицу распределения значений функции \(у = х^2\), \(х = 0,1,2,28,29\).
б) Переведите эту таблицу в таблицу распределения процентных частот.
в) Постройте круговую диаграмму распределения процентных частот.
г) Разбейте промежуток от 0 до 1000 на три промежутка так, чтобы каждому из них принадлежало по 10 значений этой функции.
Рассматривается функция \( y = x^2 \) на множестве целых неотрицательных значений аргумента \(x\). Общее количество рассматриваемых значений составляет 30 (это следует из суммы частот: \(18 + 7 + 5 = 30\)). Такая выборка позволяет провести статистический анализ распределения её значений по заданным интервалам.
а) Распределение количества значений по интервалам
Значения функции \(y = x^2\) разбиты на три неравных интервала. В таблице указано, сколько из 30 вычисленных значений попадает в каждый из них:
| Промежуток | от 0 до 300 | от 300 до 600 | от 600 до 1000 |
|---|---|---|---|
| Число значений функции \( y = x^2 \) | 18 | 7 | 5 |
Пояснение: Интервалы выбраны так, чтобы отразить неравномерный рост квадратичной функции. Большинство значений (18 из 30) сосредоточены в самом нижнем диапазоне (0–300), что характерно для функции \(x^2\): при малых \(x\) значения \(y\) растут медленно, а затем ускоряются.
б) Частота значений в процентах
Чтобы оценить долю каждого интервала в общей выборке, переведём абсолютные числа в проценты. Общее количество значений: 30.
| Промежуток | от 0 до 300 | от 300 до 600 | от 600 до 1000 |
|---|---|---|---|
| Частота значений функции \( y = x^2, \% \) | 60 | 23,3 | 16,7 |
Проверка расчётов:
- Для 0–300: \( \frac{18}{30} \times 100\% = 60\% \)
- Для 300–600: \( \frac{7}{30} \times 100\% \approx 23{,}3\% \)
- Для 600–1000: \( \frac{5}{30} \times 100\% \approx 16{,}7\% \)
Сумма: \(60\% + 23{,}3\% + 16{,}7\% = 100\%\), что подтверждает корректность расчётов.
в) Построим круговую диаграмму распределения частот.
Круговая диаграмма наглядно показала бы, что более половины всех значений (60%) лежат в первом интервале, а остальные распределены между двумя верхними. Однако, согласно условию, диаграмма здесь не приводится.
г) Пример другого разбиения на интервалы
Вместо равномерного или пропорционального разбиения можно использовать и другие подходы. Например, можно выделить очень узкий начальный интервал, чтобы детальнее рассмотреть область малых значений:
Например: от 0 до 99; от 99 до 399; от 399 до 1000.
Такое разбиение может быть полезно, если нас интересует поведение функции вблизи нуля, где изменения происходят наиболее медленно.
Общий вывод: Квадратичная функция \(y = x^2\) демонстрирует неравномерное распределение своих значений: плотность значений выше при малых \(x\) и снижается по мере роста \(x\). Это свойство важно учитывать при статистическом анализе, моделировании и выборе шкал для графиков.