Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 47.4 Мордкович — Подробные Ответы
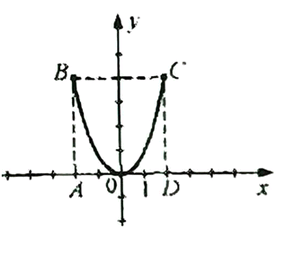
Постройте прямоугольник с вершинами в точках А(-2; 0), В(-2; 4), С(2; 4), D(2; 0). а) Сколько точек, у которых обе координаты — целые числа, принадлежит полученному прямоугольнику (включая его границы)? б) Изобразите часть графика функции у = x², которая принадлежит этому прямоугольнику. в) Сколько точек из пункта а) лежит ниже графика; на графике; выше графика? Заполните таблицу распределения точек:
а) 25 (5 · 5) точек.
б)
в)
| Положение точки | Ниже графика | На графике | Выше графика |
|---|---|---|---|
| Число точек | 10 | 5 | 10 |
Рассматривается задача анализа взаимного расположения точек координатной сетки и графика некоторой функции (например, \(y = x^2\) или другой). Сетка состоит из целочисленных точек в определённой области.
а) Общее количество точек
Сетка образована пересечением 5 горизонтальных и 5 вертикальных линий, что даёт:
5 · 5 = 25 точек.
Это полное множество точек, которые будут анализироваться в дальнейшем.
б) График функции
На координатной плоскости построен график некоторой функции. Он разделяет плоскость на две области: точки, лежащие выше графика, и точки, лежащие ниже него. Точки, координаты которых точно удовлетворяют уравнению функции, лежат на графике.
в) Распределение точек по отношению к графику
Каждая из 25 точек была классифицирована по её положению относительно графика функции. Результаты сведены в таблицу:
| Положение точки | Ниже графика | На графике | Выше графика |
|---|---|---|---|
| Число точек | 10 | 5 | 10 |
Анализ: Распределение симметрично: по 10 точек находятся выше и ниже графика. Это может указывать на то, что функция является чётной (например, \(y = x^2\)) или имеет другую форму симметрии. Пять точек лежат непосредственно на графике, что означает, что их координаты являются решениями уравнения функции.
Проверка: Общее количество точек: \(10 + 5 + 10 = 25\), что совпадает с результатом из пункта а). Это подтверждает корректность подсчётов.
Вывод: Такой анализ позволяет визуально и количественно оценить, как график функции проходит через заданную сетку точек. Это полезный инструмент для понимания поведения функции и проверки её свойств (монотонность, симметрия, выпуклость).