ГДЗ по Алгебре 7 Класс Номер 5.15 Мордкович — Подробные Ответы

По названию числового промежутка запишите его обозначение, постройте геометрическую и аналитическую модели: а) Открытый луч с началом в точке 5; б) луч с началом в точке -2; в) интервал с началом в точке 1 и концом в точке 3; г) полуинтервал с началом в точке 6 и концом в точке 10 (рассмотрите два случая).

а)
\( (5; +\infty) \)

\( x > 5 \)

б)
\( [-2; +\infty) \)

\( x \geq -2 \)

в)
\( (1; 3) \)

\( 1 < x < 3 \)

г)
\( [6; 10) \)

\( 6 \leq x < 10 \)

\( (6; 10] \)

\( 6 < x \leq 10 \)

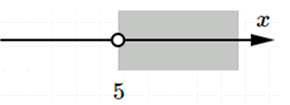
а) Открытый луч с началом в точке 5:
Обозначение: \( (5; +\infty) \)

Геометрическая модель: луч на числовой прямой, начинающийся в точке 5 (не включительно) и идущий вправо до бесконечности.
Аналитическая модель: \( x > 5 \)

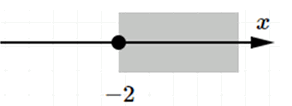
б) Луч с началом в точке -2:
Обозначение: \( [-2; +\infty) \)

Геометрическая модель: луч на числовой прямой, начинающийся в точке -2 (включительно) и идущий вправо до бесконечности.
Аналитическая модель: \( x \geq -2 \)

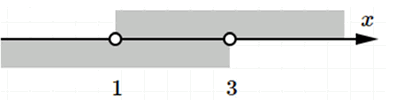
в) Интервал с началом в точке 1 и концом в точке 3:
Обозначение: \( (1; 3) \)

Геометрическая модель: отрезок на числовой прямой между точками 1 и 3 (не включительно).
Аналитическая модель: \( 1 < x < 3 \)

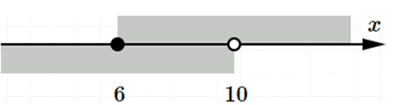
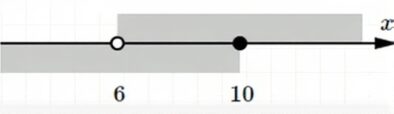
г) Полуинтервал с началом в точке 6 и концом в точке 10 (два случая):
Случай 1: Начало включается, конец не включается.
Обозначение: \( [6; 10) \)

Геометрическая модель: отрезок на числовой прямой между точками 6 (включительно) и 10 (не включительно).
Аналитическая модель: \( 6 \leq x < 10 \)

Случай 2: Начало не включается, конец включается.
Обозначение: \( (6; 10] \)

Геометрическая модель: отрезок на числовой прямой между точками 6 (не включительно) и 10 (включительно).
Аналитическая модель: \( 6 < x \leq 10 \)

а)
\( (5; +\infty) \), \( x > 5 \)

б)
\( [-2; +\infty) \), \( x \geq -2 \)

в)
\( (1; 3) \), \( 1 < x < 3 \)

г)
\( [6; 10) \), \( 6 \leq x < 10 \) или \( (6; 10] \), \( 6 < x \leq 10 \)