Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 5.39 Мордкович — Подробные Ответы
Обоснуйте с помощью координатной прямой утверждение: если а > b, то -а < -b. Рассмотрите следующие случаи: а) а и b — положительные числа; б) а и b — отрицательные числа; в) а — положительное число, b — отрицательное число; г) \(а = 0, b — отрицательное число. \)
а)
\( a > b > 0 \)
\( a = b + c, \; c > 0 \)
\( -a = -b — c \)
\( -a < -b \)
б)
\( 0 > a > b \)
\( a = b + c, \; c > 0 \)
\( -a = -b — c \)
\( -a > -b \)
в)
\( a > 0 > b \)
\( -a < 0 < -b \)
\( -a < -b \)
г)
\( a = 0 > b \)
\( -a = 0 \)
\( -b > 0 \)
\( -a < -b \)
Условие: Доказать, что если \(a > b\) , то \(-a < -b\) для разных случаев знаков \(a\) и \(b\).
Решение:
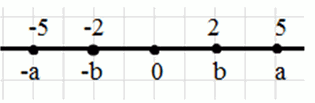
а)
\(a\) и \(b\)— положительные числа:
\(a > b > 0\) — дано
На координатной прямой \(a\)
правее \(b\).
\(-a < -b < 0\) — умножаем на -1
На координатной прямой \(-a\)
левее \(-b\).
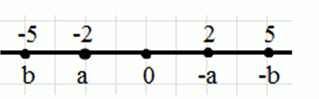
б)
\(a\) и \(b\) — отрицательные числа:
\(0 > a > b\) — дано
На координатной прямой \(a\)
правее \(b\).
\(0 < -a < -b\) — умножаем на -1
На координатной прямой \(-a\)
левее \(-b\).
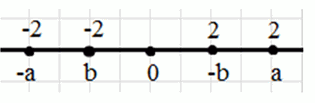
в)
\(a\) — положительное, \(b\) — отрицательное:
\(a > 0 > b\) — дано
На координатной прямой \(a\) правее \(b\).
\(-a < 0 < -b\)— умножаем на -1
На координатной прямой \(-a\) левее \(-b\).
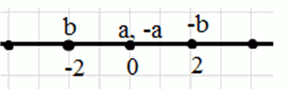
г)
\(a = 0\), \(b\)— отрицательное: \(0 > b\) — дано, \(a = 0\)
На координатной прямой \(0\) правее \(b\).
\(-0 < -b\)— умножаем на -1
\(0 < -b\) — упрощаем
На координатной прямой \(0\) левее \(-b\).
Утверждение доказано для всех рассмотренных случаев.