Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 5.42 Мордкович — Подробные Ответы
а) Изобразите множество точек координатной прямой, расстояние до которых от точки O(0) меньше трёх единичных отрезков. б) Изобразите множество точек координатной прямой, расстояние до которых от точки А(а) больше двух единичных отрезков. в) Изобразите множество точек координатной прямой, расстояние до которых от точки O(0) больше трёх единичных отрезков. г) Изобразите множество точек координатной прямой, расстояние до которых от точки А(а) меньше двух единичных отрезков.
а)
\( |x| < 3 \)
\( -3 < x < 3 \)
б)
\( |x — a| > 2 \)
\( x — a > 2 \) или \( x — a < -2 \)
\( x > a + 2 \) или \( x < a — 2 \)
в)
\( |x| > 3 \)
\( x > 3 \) или \( x < -3 \)
г)
\( |x — a| < 2 \)
\( -2 < x — a < 2 \)
\( a — 2 < x < a + 2 \)
Условие:
Изобразить множества точек на прямой, удовлетворяющих условиям расстояния от заданных точек.
Решение:
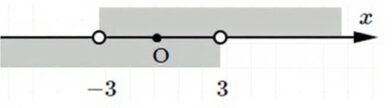
а) Расстояние от O(0) меньше 3:
\( |x — 0| < 3 \) — условие
\( -3 < x < 3 \) — интервал
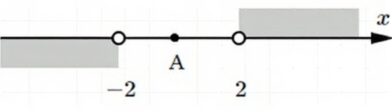
б) Расстояние от A(a) больше 2:
\( |x — a| > 2 \) — условие
\( x — a > 2 \) или \( x — a < -2 \) — раскрываем модуль
\( x > a + 2 \) или \( x < a — 2 \)— интервалы
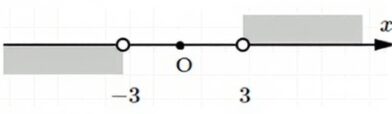
в) Расстояние от O(0) больше 3:
\( |x — 0| > 3 \) — условие
\( x > 3 \) или \( x < -3 \) — интервалы
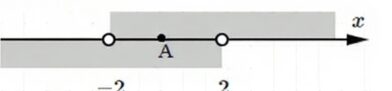
г) Расстояние от A(a) меньше 2:
\( |x — a| < 2 \) — условие
\( -2 < x — a < 2 \) — раскрываем модуль
\( a — 2 < x < a + 2 \) — интервал
а)
\( -3 < x < 3 \)
б)
\( x > a + 2 \) или \( x < a — 2 \)
в)
\( x > 3 \) или \( x < -3 \)
г)
\( a — 2 < x < a + 2 \)