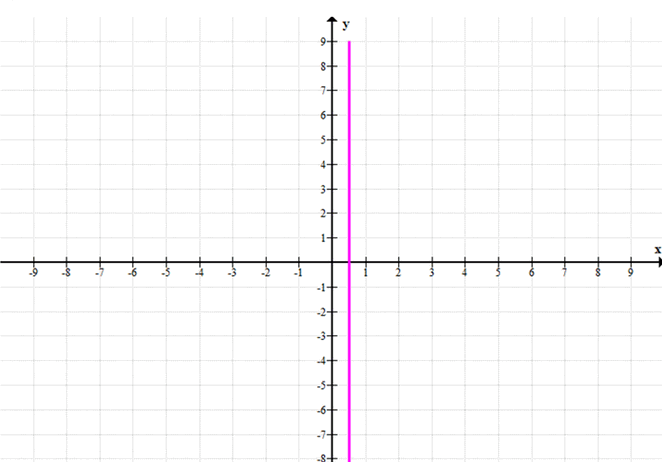ГДЗ по Алгебре 7 Класс Номер 7.13 Мордкович — Подробные Ответы

а) \(х = 0,5\); б) \(у = -1,5\); в) \(у = 3,5\); г) \(х = -6,5. \)

a)
\( x = 0,5 \)

б)
\( y = -1,5 \)

в)
\( y = 3,5 \)

г)
\( x = -6,5 \)

Задача

Найдите аналитические модели прямых, заданных уравнениями:

a) \(x = 0.5\)
б) \(y = -1.5\)
в) \(y = 3.5\)
г) \(x = -6.5\)

Решение

a) \(x = 0.5\)

Описание: Это уравнение представляет вертикальную прямую, которая проходит через точку с абсциссой 0.5.

— Графическое представление: Все точки на этой прямой имеют координаты вида \((0.5; y)\), где \(y\) может принимать любые значения.
— Примеры точек:
— (0.5; 2)
— (0.5; -1)
— (0.5; 4)

Аналитическая модель: Прямая описывается уравнением \(x = 0.5\).

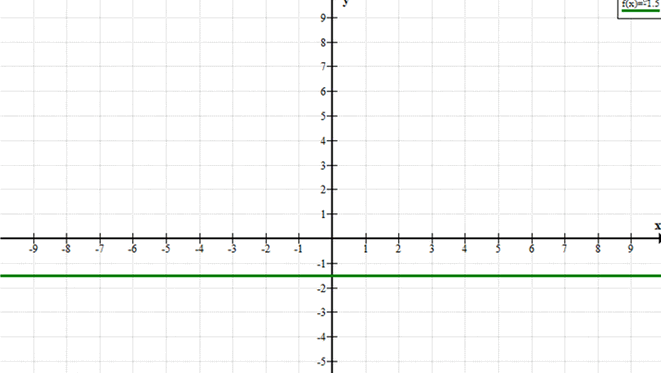
б) \(y = -1.5\)

Описание: Это уравнение представляет горизонтальную прямую, которая проходит через точку с ординатой -1.5.

— Графическое представление: Все точки на этой прямой имеют координаты вида \((x; -1.5)\), где \(x\) может принимать любые значения.
— Примеры точек:
— (1; -1.5)
— (0; -1.5)
— (-3; -1.5)

Аналитическая модель: Прямая описывается уравнением \(y = -1.5\).

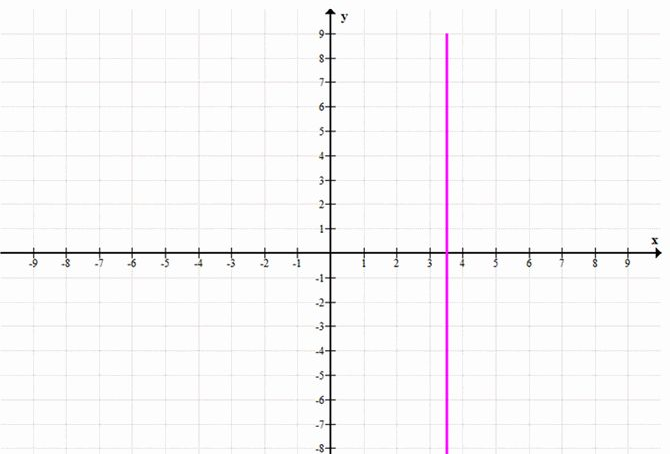
в) \(y = 3.5\)

Описание: Это уравнение также представляет горизонтальную прямую, которая проходит через точку с ординатой 3.5.

— Графическое представление: Все точки на этой прямой имеют координаты вида \((x; 3.5)\), где \(x\) может принимать любые значения.
— Примеры точек:
— (2; 3.5)
— (4; 3.5)
— (-1; 3.5)

Аналитическая модель: Прямая описывается уравнением \(y = 3.5\).

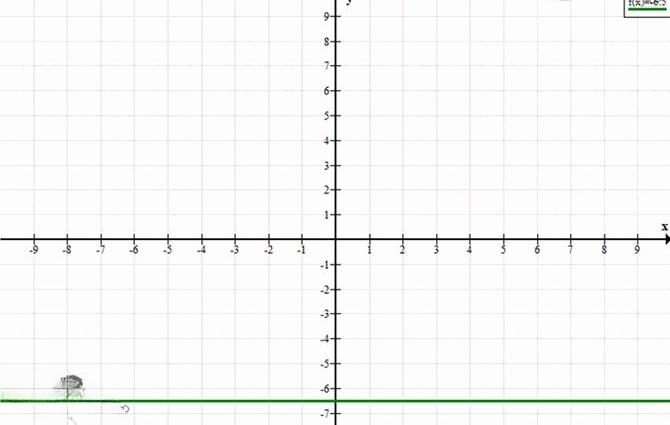
г) \(x = -6.5\)

Описание: Это уравнение представляет вертикальную прямую, которая проходит через точку с абсциссой -6.5.

— Графическое представление: Все точки на этой прямой имеют координаты вида \((-6.5; y)\), где \(y\) может принимать любые значения.
— Примеры точек:
— (-6.5; 0)
— (-6.5; -3)
— (-6.5; 5)

Аналитическая модель: Прямая описывается уравнением \(x = -6.5\).