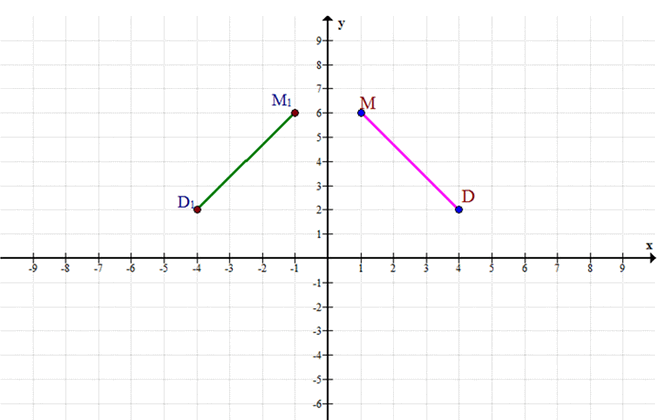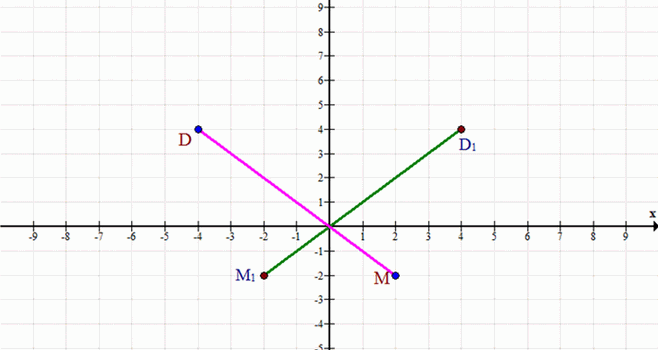Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 7.26 Мордкович — Подробные Ответы
Постройте отрезок, симметричный отрезку DM относительно оси у, если: а) D (4; 2), М( 1; 6); б) D(-3; 0), М(0; -3); в) D(-5; -3), М( 1; -2); г) D(-4; 4), М(2; -2).
а)
\(D(4; 2), M(1; 6)\)
\(D'(-4; 2), M'(-1; 6)\)
б)
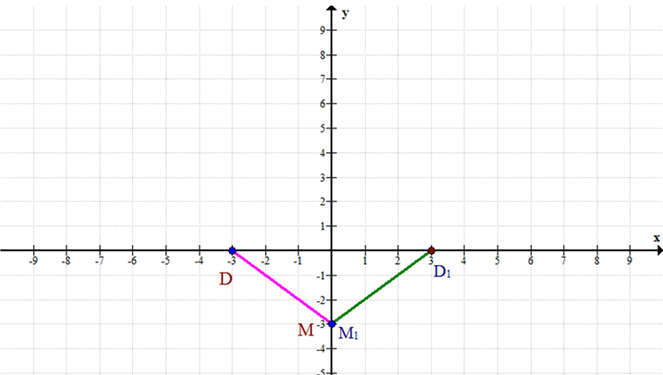
\(D(-3; 0), M(0; -3)\)
\(D'(3; 0), M'(0; -3)\)
в)
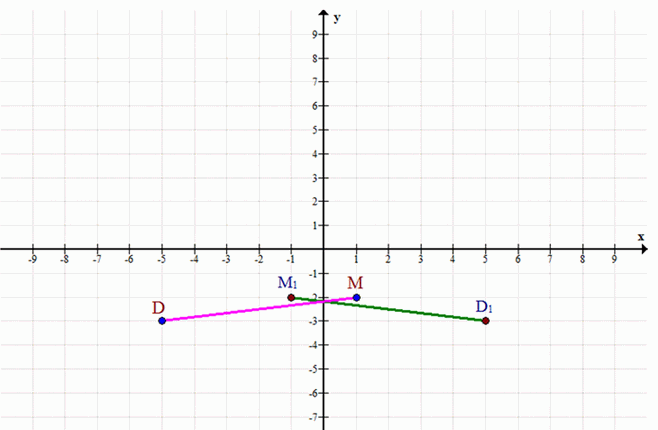
\(D(-5; -3), M(1; -2)\)
\(D'(5; -3), M'(-1; -2)\)
г)
\(D(-4; 4), M(2; -2)\)
\(D'(4; 4), M'(-2; -2)\)
Условие:
Построить отрезок, симметричный отрезку DM относительно оси y для заданных координат точек D и M.
Решение:
а) D(4; 2), M(1; 6)
\(D'(-4; 2)\)
— симметрия точки D относительно оси y
\(M'(-1; 6)\)
— симметрия точки M относительно оси y
б) D(-3; 0), M(0; -3)
\(D'(3; 0)\)
— симметрия точки D относительно оси y
\(M'(0; -3)\)
— симметрия точки M относительно оси y
в) D(-5; -3), M(1; -2)
\(D'(5; -3)\)
— симметрия точки D относительно оси y
\(M'(-1; -2)\)
— симметрия точки M относительно оси y
г) D(-4; 4), M(2; -2)
\(D'(4; 4)\)
— симметрия точки D относительно оси y
\(M'(-2; -2)\)
— симметрия точки M относительно оси y
а) D'(-4; 2), M'(-1; 6)
б) D'(3; 0), M'(0; -3)
в) D'(5; -3), M'(-1; -2)
г) D'(4; 4), M'(-2; -2)