Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 7.35 Мордкович — Подробные Ответы
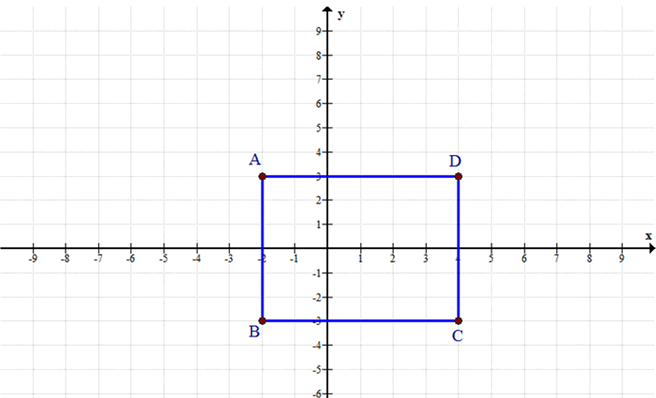
Длина стороны квадрата ABCD равна 6, а координаты вершины А равны (-2; 3). Найдите координаты остальных вершин, зная, что сторона АВ квадрата параллельна оси ординат и что начало координат лежит внутри квадрата.
\( A(-2; 3) \)
\( AB = 6 \)
\( AB \parallel Oy \)
\( B(-2; 3+6) = B(-2; -3) \)
\( C(-2+6; 9) = C(4; -3) \)
\( D(-2+6; 3) = D(4; 3) \)
Условие:
Квадрат ABCD, сторона 6, A(-2; 3), AB || оси Oy, начало координат внутри квадрата. Найти координаты B, C, D.
Решение:
Так как AB || оси Oy, то \(x_B = x_A = -2\).
\(y_B = y_A + 6 = 3 — 6 = -3\) — координата B
Координаты точки B: \((-2; -3)\)
Так как ABCD — квадрат, то BC || оси Ox, и \(y_C = y_B = 9\).
\(x_C = x_B + 6 = -2 + 6 = 4\) — координата C
Координаты точки C: \((4; -3)\)
Так как CD || оси Oy, то \(x_D = x_C = 4\).
\(y_D = y_C — 6 = 9 — 6 = 3\) — координата D
Координаты точки D: \((4; 3)\)
Ответ: B(-2; -3), C(4; -3), D(4; 3)