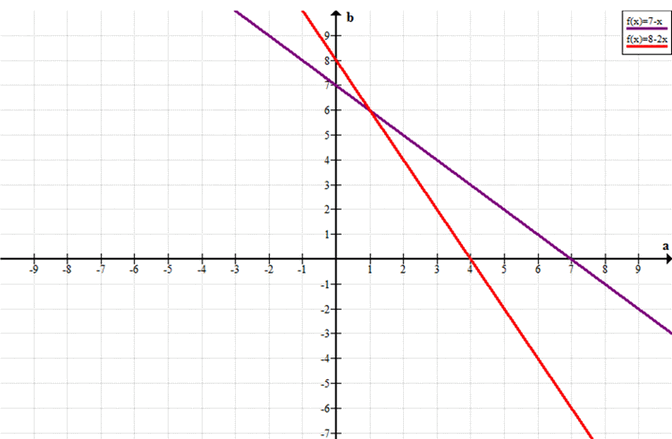Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 8.31 Мордкович — Подробные Ответы
Сумма двух чисел равна 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в сумме эти числа дадут 8. Найдите исходные числа.
\(
\begin{cases}
x + y = 7 \\
2x + y = 8
\end{cases}
\)
1)
\( 2x + y — (x + y) = 8 — 7 \)
\( x = 1 \)
2)
\( 1 + y = 7 \)
\( y = 6 \)
Условие:
Сумма двух чисел равна 7, после увеличения одного из них в 2 раза сумма стала 8. Найти исходные числа.
Решение:
Пусть \(x\) и \(y\) — исходные числа.
\( x + y = 7 \)
— первое уравнение
\( 2x + y = 8 \)
— второе уравнение
Выразим \(y\)
из первого уравнения:
\( y = 7 — x \)
Подставим выражение для \(y\)
во второе уравнение:
\( 2x + (7 — x) = 8 \)
Упростим и решим уравнение относительно \(x\):
\( 2x + 7 — x = 8 \)
\( x = 8 — 7 \)
\( x = 1 \)
Найдем \(y\):
\( y = 7 — x = 7 — 1 = 6 \)