Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 9.20 Мордкович — Подробные Ответы
Постройте график линейной функции в соответствующей системе координат: а) \(у = -х + 2\); б) \(у = -х — 3\); в) \(у = -х + 1\); г) \(y = -х — 8. \)
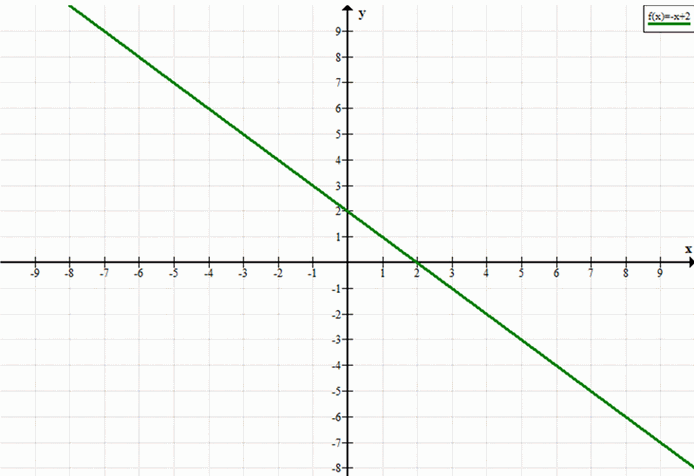
а) Уравнение: \( y = -x + 2 \)
1. Наклон (k): Угловой коэффициент равен -1. Это означает, что график будет наклонен вниз.
2. Пересечение с осью \(y\) (m): Свободный член равен 2. График пересекает ось \(y\) в точке (0, 2).
3. Точки для построения:
— При \( x = 0 \): \( y = 2 \) → точка (0, 2)
— При \( x = 2 \): \( y = -2 + 2 = 0 \) → точка (2, 0)
— При \( x = -2 \): \( y = 2 + 2 = 4 \) → точка (-2, 4)
График: Линия будет проходить через точки (0, 2) и (2, 0), наклоняясь вниз.
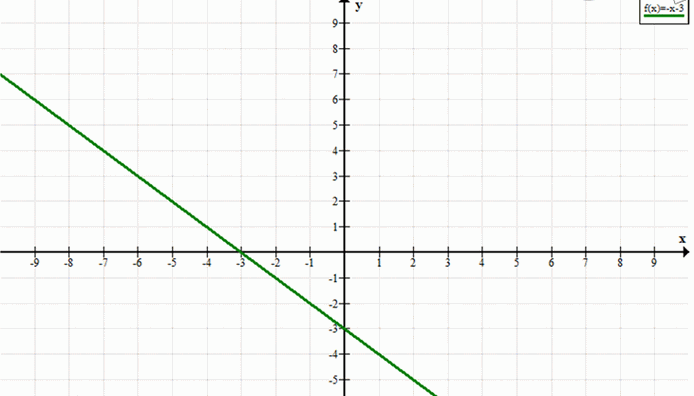
б) Уравнение: \( y = -x — 3 \)
1. Наклон (k): Угловой коэффициент равен -1. График также будет наклонен вниз.
2. Пересечение с осью \(y\) (m): Свободный член равен -3. График пересекает ось \(y\) в точке (0, -3).
3. Точки для построения:
— При \( x = 0 \): \( y = -3 \) → точка (0, -3)
— При \( x = 2 \): \( y = -2 — 3 = -5 \) → точка (2, -5)
— При \( x = -2 \): \( y = 2 — 3 = -1 \) → точка (-2, -1)
График: Линия будет проходить через точки (0, -3) и (2, -5), наклоняясь вниз.
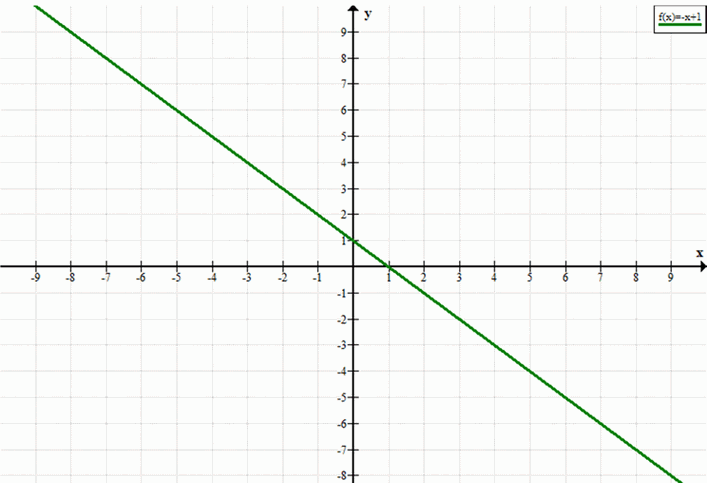
в) Уравнение: \( y = -x + 1 \)
1. Наклон (k): Угловой коэффициент равен -1. График будет наклонен вниз.
2. Пересечение с осью \(y\) (m): Свободный член равен 1. График пересекает ось \(y\) в точке (0, 1).
3. Точки для построения:
— При \( x = 0 \): \( y = 1 \) → точка (0, 1)
— При \( x = 1 \): \( y = -1 + 1 = 0 \) → точка (1, 0)
— При \( x = -1 \): \( y = 1 + 1 = 2 \) → точка (-1, 2)
График: Линия будет проходить через точки (0, 1) и (1, 0), наклоняясь вниз.
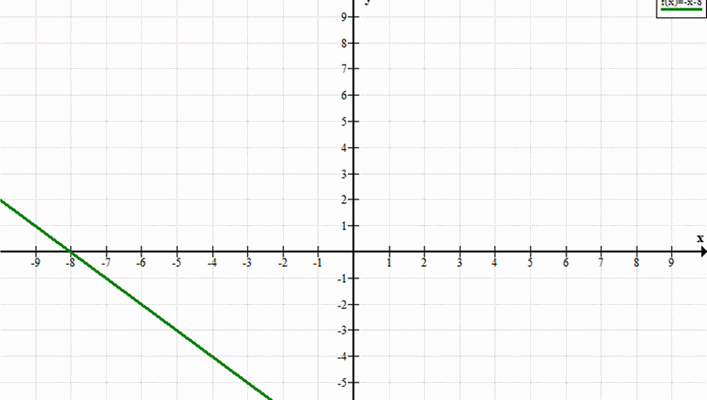
г) Уравнение: \( y = -x — 8 \)
1. Наклон (k): Угловой коэффициент равен -1. График будет наклонен вниз.
2. Пересечение с осью \(y\) (m): Свободный член равен -8. График пересекает ось \(y\) в точке (0, -8).
3. Точки для построения:
— При \( x = 0 \): \( y = -8 \) → точка (0, -8)
— При \( x = 2 \): \( y = -2 — 8 = -10 \) → точка (2, -10)
— При \( x = -2 \): \( y = 2 — 8 = -6 \) → точка (-2, -6)
График: Линия будет проходить через точки (0, -8) и (2, -10), наклоняясь вниз.
Общая информация о графиках
— Все графики являются прямыми линиями, так как мы имеем дело с линейными функциями.
— Угловой коэффициент определяет наклон линии: все функции имеют отрицательный угловой коэффициент, что означает, что линии будут наклонены вниз.
— Свободный член определяет точку пересечения с осью \(y\): это значение \( y \), когда \( x = 0 \).
Пояснение графиков
— График функции: Каждая функция будет представлена на координатной плоскости, где ось \(x\) — горизонтальная, а ось \(y\) — вертикальная. Линии будут пересекаться с осью \(y\) в указанных точках и наклоняться вниз вправо.
— Проверка точек: Для более точного построения графиков можно выбрать дополнительные значения \( x \) и вычислить соответствующие значения \( y \), чтобы получить больше точек для построения линии.