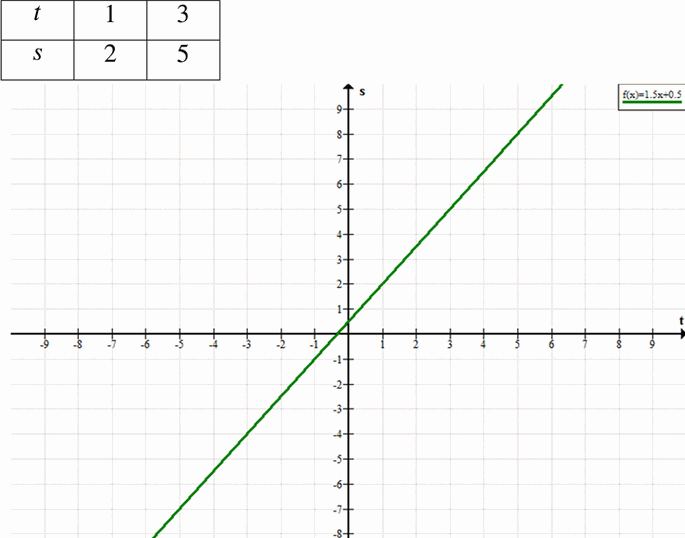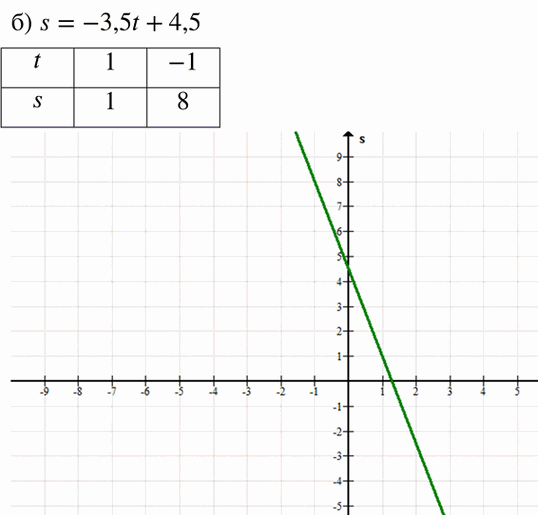Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 9.25 Мордкович — Подробные Ответы
Постройте график линейной функции в соответствующей системе координат: a) \(s = 1,5t + 0,5\); 6) \(s = -3,5t + 4,5\); в) \(s = -4,5t — 2,5\); г) \(s = 2,5t — 3,5. \)
a)
\( t = 2 \)
\( s = 1,5 \cdot 2 + 0,5 \)
\( s = 3 + 0,5 \)
\( s = 3,5 \)
б)
\( t = 2 \)
\( s = -3,5 \cdot 2 + 4,5 \)
\( s = -7 + 4,5 \)
\( s = -2,5 \)
в)
\( t = 2 \)
\( s = -4,5 \cdot 2 — 2,5 \)
\( s = -9 — 2,5 \)
\( s = -11,5 \)
г)
\( t = 2 \)
\( s = 2,5 \cdot 2 — 3,5 \)
\( s = 5 — 3,5 \)
\( s = 1,5 \)
a) Уравнение: \( s = 1.5t + 0.5 \)
— Наклон (k): 1.5
— Пересечение с осью \(s\): (0, 0.5)
— Точки:
— \( t = 0 \): \( s = 0.5 \) → (0, 0.5)
— \( t = 2 \): \( s = 1.5(2) + 0.5 = 3 + 0.5 = 3.5 \) → (2, 3.5)
— \( t = -2 \): \( s = 1.5(-2) + 0.5 = -3 + 0.5 = -2.5 \) → (-2, -2.5)
б) Уравнение: \( s = -3.5t + 4.5 \)
— Наклон (k): -3.5
— Пересечение с осью \(s\): (0, 4.5)
— Точки:
— \( t = 0 \): \( s = 4.5 \) → (0, 4.5)
— \( t = 1 \): \( s = -3.5(1) + 4.5 = -3.5 + 4.5 = 1 \) → (1, 1)
— \( t = -1 \): \( s = -3.5(-1) + 4.5 = 3.5 + 4.5 = 8 \) → (-1, 8)
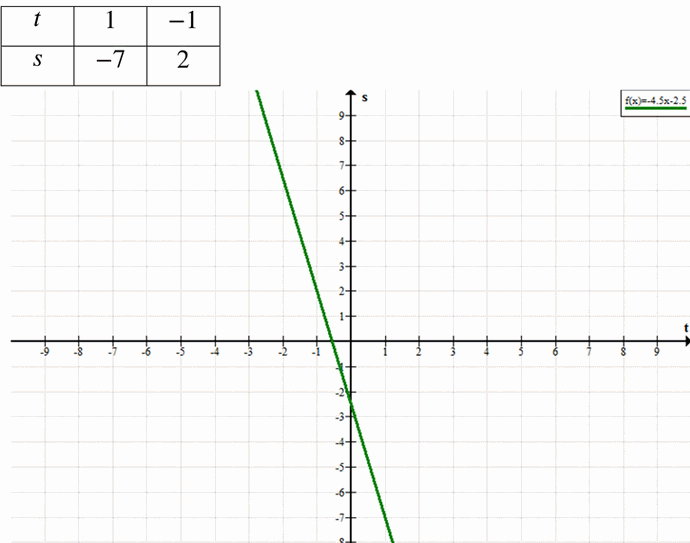
в) Уравнение: \( s = -4.5t — 2.5 \)
— Наклон (k): -4.5
— Пересечение с осью \(s\): (0, -2.5)
— Точки:
— \( t = 0 \): \( s = -2.5 \) → (0, -2.5)
— \( t = 2 \): \( s = -4.5(2) — 2.5 = -9 — 2.5 = -11.5 \) → (2, -11.5)
— \( t = -2 \): \( s = -4.5(-2) — 2.5 = 9 — 2.5 = 6.5 \) → (-2, 6.5)
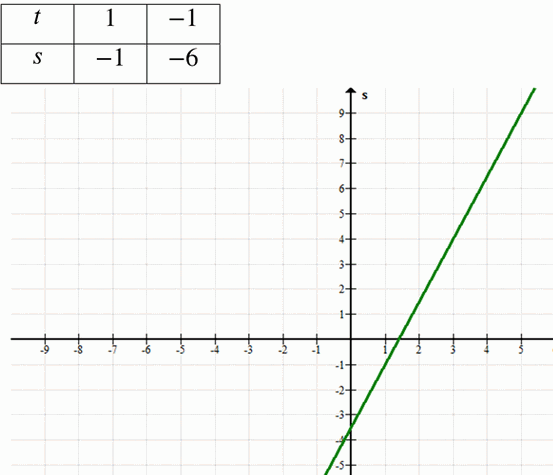
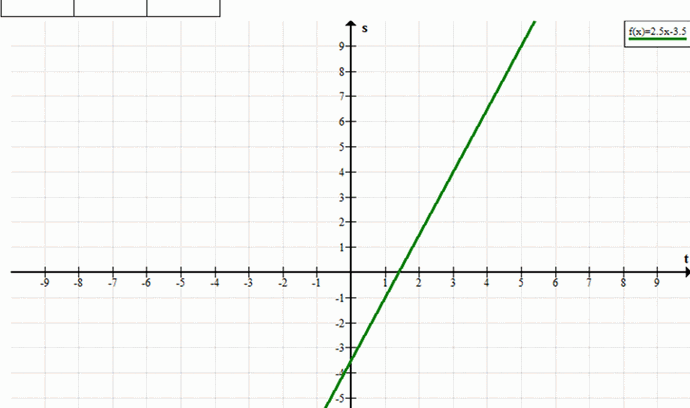
г) Уравнение: \( s = 2.5t — 3.5 \)
— Наклон (k): 2.5
— Пересечение с осью \(s\): (0, -3.5)
— Точки:
— \( t = 0 \): \( s = -3.5 \) → (0, -3.5)
— \( t = 2 \): \( s = 2.5(2) — 3.5 = 5 — 3.5 = 1.5 \) → (2, 1.5)
— \( t = -2 \): \( s = 2.5(-2) — 3.5 = -5 — 3.5 = -8.5 \) → (-2, -8.5)
Итоговые графики
— Все графики будут прямыми линиями, наклоненными вверх или вниз в зависимости от углового коэффициента.
— Для функций \( s = 1.5t + 0.5 \) и \( s = 2.5t — 3.5 \) линии поднимаются, так как угловые коэффициенты положительные.
— Для функций \( s = -3.5t + 4.5 \) и \( s = -4.5t — 2.5 \) линии наклоняются вниз, так как угловые коэффициенты отрицательные.
Пересечения с осью \(s\) находятся в точках \( (0, 0.5) \), \( (0, 4.5) \), \( (0, -2.5) \) и \( (0, -3.5) \) соответственно для каждой функции.