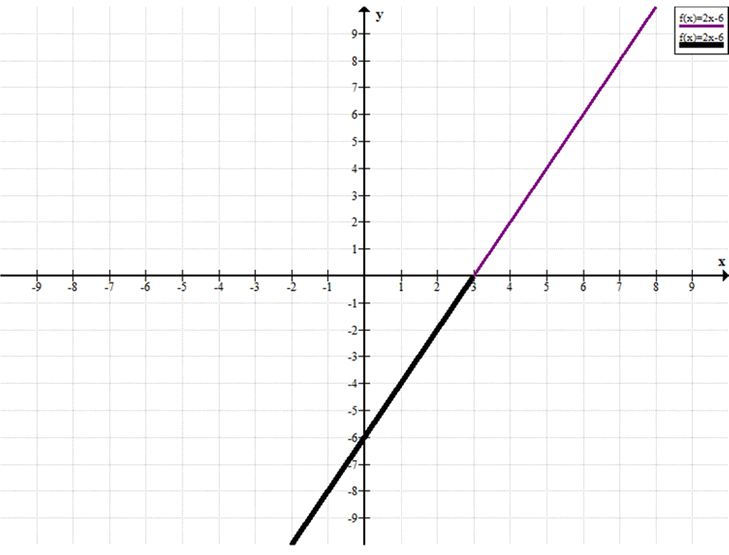Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 9.33 Мордкович — Подробные Ответы
Постройте график функции у = 2x — 6. а) С помощью построенного графика решите уравнение 2x — 6 = 0. б) Выделите ту часть графика, которая соответствует условию у < 0. При каких значениях аргумента функция принимает отрицательные значения? в) С помощью графика решите неравенство 2x — 6 < = 0. г) Решите неравенство 2x — 6 > = 0.
\( y = 2x — 6 \)
а)
\( 2x — 6 = 0 \)
\( 2x = 6 \)
\( x = 3 \)
б)
\( y < 0 \)
\( 2x — 6 < 0 \)
\( 2x < 6 \)
\( x < 3 \)
в)
\( 2x — 6 \le 0 \)
\( 2x \le 6 \)
\( x \le 3 \)
г)
\( 2x — 6 \ge 0 \)
\( 2x \ge 6 \)
\( x \ge 3 \)
График функции \(y = 2x — 6\)
— прямая.
Для построения прямой достаточно двух точек:
\(x = 0, y = -6\)
— первая точка \((0, -6)\)
\(x = 3, y = 0\)
— вторая точка \((3, 0)\)
а) Решение уравнения \(2x — 6 = 0\) графически:
Находим точку пересечения графика с осью \(x\).
\(y = 0\) при \(x = 3\)
б) Область \(y < 0\):
График ниже оси \(x\) при \(x < 3\)
Функция принимает отрицательные значения при \(x < 3\)
в) Решение неравенства \(2x — 6 \le 0\)
графически: Находим значения \(x\), при которых график ниже или на оси \(x\).
\(x \le 3\)
г) Решение неравенства \(2x — 6 \ge 0\)
графически:
Находим значения \(x\), при которых график выше или на оси \(x\).
\(x \ge 3\)
Ответы:
а)
\(x = 3\)
б)
\(x < 3\)
в)
\(x \le 3\)
г)
\(x \ge 3\)