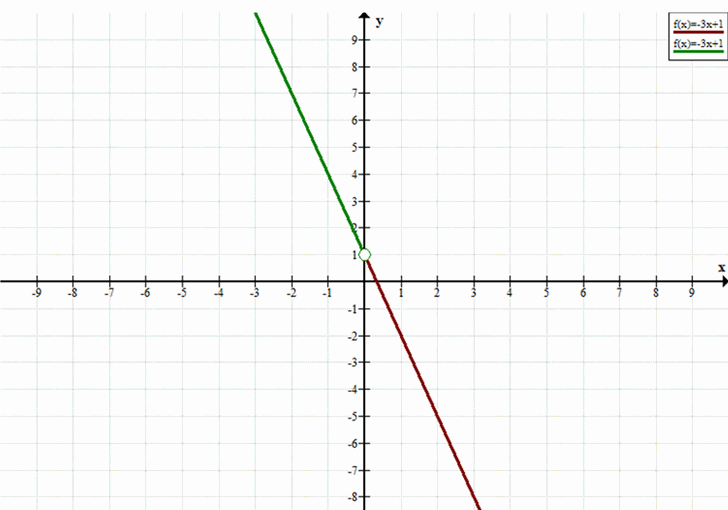ГДЗ по Алгебре 7 Класс Номер 9.43 Мордкович — Подробные Ответы

Постройте график линейной функции у = -3х + 1 и выделите его часть, соответствующую заданному промежутку оси x: а) (-∞; 0]; б) (2; +∞); в) (-∞; 0); г) [1; +∞).

а)
\( (-\infty; 0] \)

б)
\( (2; +\infty) \)

в)
\( (-\infty; 0) \)

г)
\( [1; +\infty) \)

Для построения графика линейной функции \( y = -3x + 1 \) и выделения его части в заданных промежутках оси \( x \), начнем с определения ключевых характеристик функции и построения графика.

1. Построение графика функции \( y = -3x + 1 \)

— Угловой коэффициент \( k = -3 \) указывает на то, что график будет наклонен вниз.
— Свободный член \( m = 1 \) показывает, что график пересекает ось \( y \) в точке (0, 1).

Точки для построения графика:

— При \( x = 0 \):
\[
y = -3(0) + 1 = 1 \quad \text{→ точка (0, 1)}
\]

— При \( x = 1 \):
\[
y = -3(1) + 1 = -2 \quad \text{→ точка (1, -2)}
\]

— При \( x = 2 \):
\[
y = -3(2) + 1 = -5 \quad \text{→ точка (2, -5)}
\]

— При \( x = -1 \):
\[
y = -3(-1) + 1 = 4 \quad \text{→ точка (-1, 4)}
\]

— При \( x = -2 \):
\[
y = -3(-2) + 1 = 7 \quad \text{→ точка (-2, 7)}
\]

Построив эти точки, мы можем провести прямую линию, которая будет представлять график функции.

2. Выделение части графика для заданных промежутков оси \( x \)

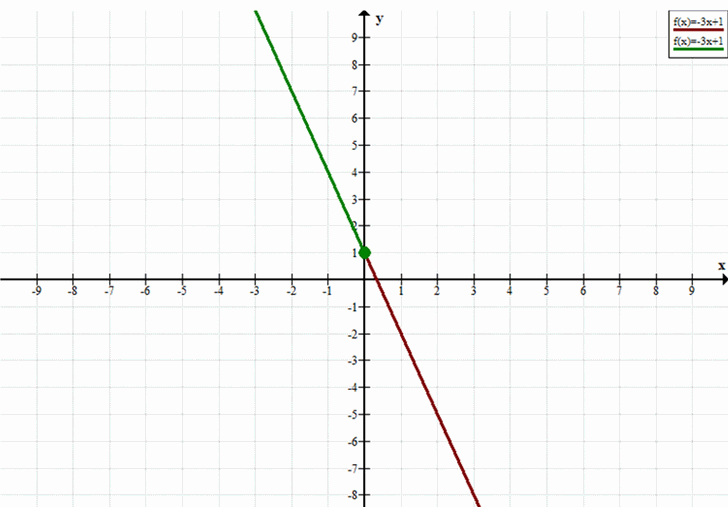
а) Промежуток \( (-\infty; 0] \)

— В этом промежутке выделяется часть графика, соответствующая значениям \( x \leq 0 \).
— На графике это будет линия от \( x = -\infty \) до точки (0, 1), включая её.

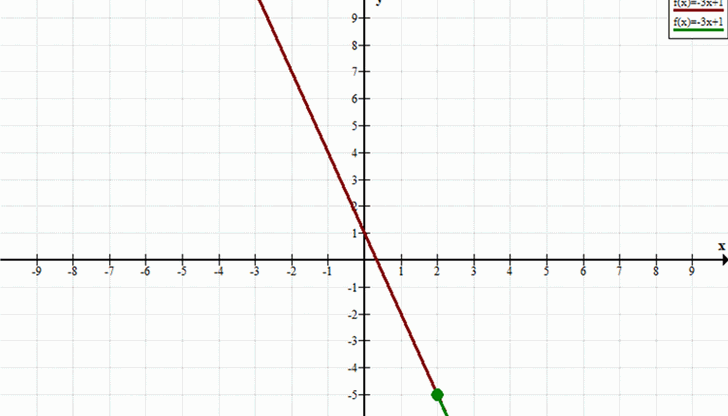
б) Промежуток \( (2; +\infty) \)

— Здесь выделяется часть графика, соответствующая значениям \( x > 2 \).
— Это будет линия, начиная от точки (2, -5) и продолжая вправо до бесконечности, не включая точку (2, -5).

в) Промежуток \( (-\infty; 0) \)

— В этом случае мы выделяем часть графика для значений \( x < 0 \).
— На графике это будет линия от \( x = -\infty \) до точки (0, 1), не включая её.

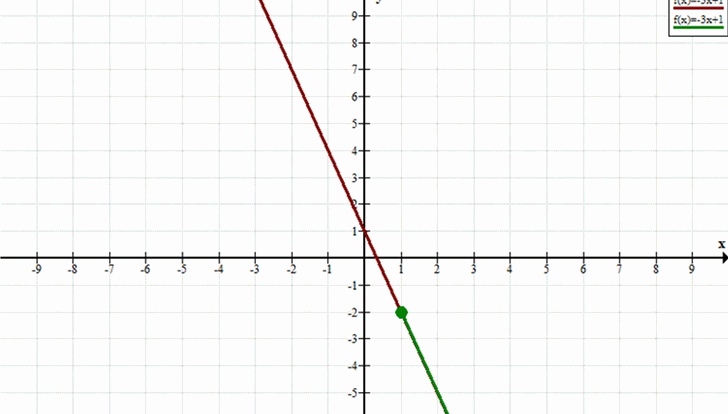
г) Промежуток \( [1; +\infty) \)

— Здесь выделяется часть графика, соответствующая значениям \( x \geq 1 \).
— Это будет линия, начиная от точки (1, -2) и продолжающейся вправо до бесконечности, включая точку (1, -2).

Итог

График функции \( y = -3x + 1 \) представляет собой прямую линию, и в зависимости от заданного промежутка оси \( x \) выделяются соответствующие части этой линии. Для каждого промежутка выделенная часть будет выглядеть следующим образом:

— Для \( (-\infty; 0] \): линия от \( x = -\infty \) до \( x = 0 \) (включая точку (0, 1)).
— Для \( (2; +\infty) \): линия от \( x = 2 \) (не включая) до \( x = +\infty \).
— Для \( (-\infty; 0) \): линия от \( x = -\infty \) до \( x = 0 \) (не включая точку (0, 1)).
— Для \( [1; +\infty) \): линия от \( x = 1 \) (включая точку (1, -2)) до \( x = +\infty \).