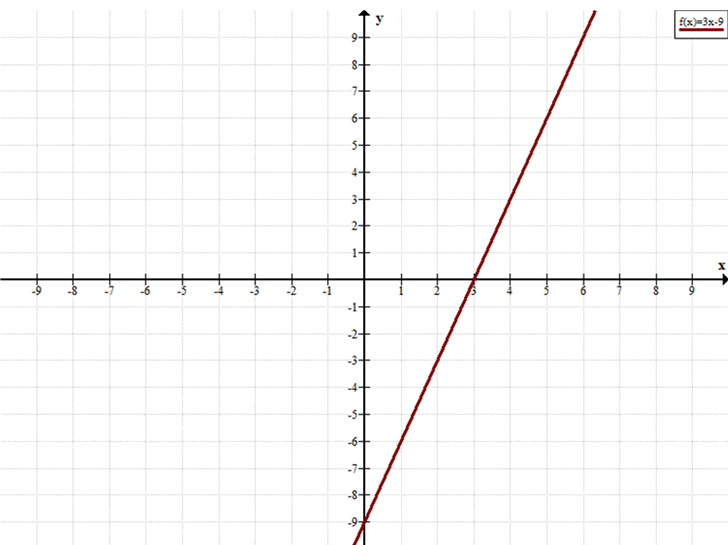Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 9.47 Мордкович — Подробные Ответы
Постройте график линейной функции у = 3х — 9 и с его помощью найдите: а) координаты точки пересечения графика с осью абсцисс; б) все значения аргумента, при которых выполняется неравенство у < 0; в) решение неравенства Зx — 9 > 0; г) значения х, при которых выполняется неравенство У > -9.
\( y = 3x — 9 \)
a)
\( y = 0 \)
\( 3x — 9 = 0 \)
\( 3x = 9 \)
\( x = 3 \)
\( (3; 0) \)
б)
\( y < 0 \)
\( 3x — 9 < 0 \)
\( 3x < 9 \)
\( x < 3 \)
\( (-\infty; 3) \)
в)
\( 3x — 9 > 0 \)
\( 3x > 9 \)
\( x > 3 \)
\( (3; +\infty) \)
г)
\( y > -9 \)
\( 3x — 9 > -9 \)
\( 3x > 0 \)
\( x > 0 \)
\( (0; +\infty) \)
График \(y = 3x — 9\)
— прямая.
Для построения прямой нужны две точки:
\(x = 0 \Rightarrow y = 3 \cdot 0 — 9 = -9\)
— первая точка \((0, -9)\)
\(y = 0 \Rightarrow 3x — 9 = 0 \Rightarrow x = 3\)
— вторая точка \((3, 0)\)
а) Координаты точки пересечения с осью абсцисс:
\(y = 0 \Rightarrow 3x — 9 = 0 \Rightarrow x = 3\)
— точка \((3, 0)\)
б) Значения \(x\)
при \(y < 0\):
\(3x — 9 < 0\)
— неравенство
\(3x < 9\)
— перенос
\(x < 3\)
— делим на 3
в) Решение неравенства \(3x — 9 > 0\):
\(3x — 9 > 0\)
— неравенство
\(3x > 9\)
— перенос
\(x > 3\)
— делим на 3
г) Значения \(x\)
при \(y > -9\):
\(3x — 9 > -9\)
— неравенство
\(3x > 0\)
— перенос
\(x > 0\)
— делим на 3
Ответы:
а)
\((3, 0)\)
б)
\(x < 3\)
в)
\(x > 3\)
г)
\(x > 0\)