Задачник по алгебре для 7-го класса, написанный Мордковичем и Александровым, является важным инструментом в обучении математике. Этот учебный материал ориентирован на развитие логического мышления и навыков решения задач у школьников. В данном обзоре мы рассмотрим основные особенности и преимущества этого задачника.
ГДЗ по Алгебре 7 Класс Номер 9.61 Мордкович — Подробные Ответы
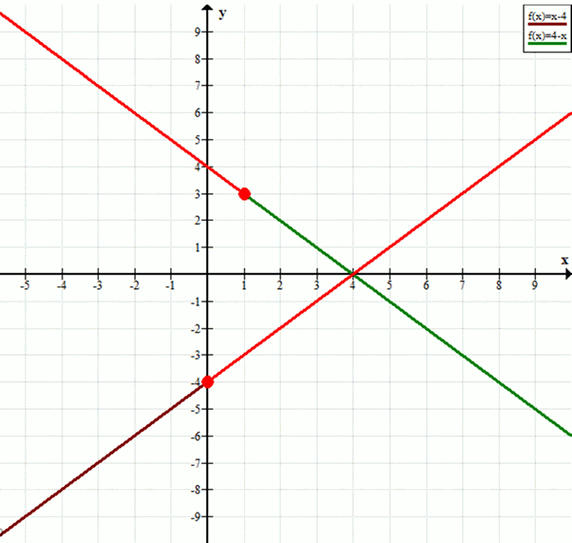
Пусть С — наименьшее значение линейной функции у = х — 4 на луче [0; +∞), a D — наименьшее значение линейной функции у = 4 — х на луче (-∞; 1]. Что больше: С или D? Сделайте графическую иллюстрацию.
\( y = x — 4 \)
\( x \in [0; +\infty) \)
\( x = 0 \)
\( y = 0 — 4 = -4 \)
\( C = -4 \)
\( y = 4 — x \)
\( x \in (-\infty; 1] \)
\( x = 1 \)
\( y = 4 — 1 = 3 \)
\( D = 3 \)
\( C < D \)
Условие:
Сравнить наименьшие значения функций \(y = x — 4\) на \([0; +\infty)\) и \(y = 4 — x\) на \((-\infty; 1]\).
Решение:
Рассмотрим функцию \(y = x — 4\) на луче \([0; +\infty)\).
\(x = 0\)
— начало луча
\(y(0) = 0 — 4 = -4\)
— значение функции в начале луча
Так как коэффициент при \(x\)
положительный, функция возрастает, значит, наименьшее значение в начале луча.
\(C = -4\)
— наименьшее значение первой функции
Рассмотрим функцию \(y = 4 — x\) на луче \((-\infty; 1]\).
\(x = 1\)
— конец луча
\(y(1) = 4 — 1 = 3\)
— значение функции в конце луча
Так как коэффициент при \(x\)
отрицательный, функция возрастает, значит, наименьшее значение в конце луча.
\(D = 3\)
— наименьшее значение второй функции
Сравним \(C\) и \(D\):
\(C = -4\)
\(D = 3\)
\(C < D\)
Ответ: D больше, чем C.